1.Draw an acute scalene triangle on a piece of paper and label it ABC.
2. Fold the paper so that A lies directly on top of C. Crease the paper and determine if there is anything special about this line?
3.Continue the activity by placing B on top of C and A on top of point B. Each time the paper crease will yield a special line. What line is this?
4. Look at the intersection of the three lines. Label this point O. What characteristics would be true of point O with regard to its distance from A, B, and C?
5. Can a circle be drawn which contains each of the vertices of this triangle? If so, draw it.
Next draw an obtuse scalene triangle and repeat the process for locating point O. The teacher should be certain that in observing the groups and their work that they have recognized that O is the point of concurrency for the three perpendicular bisectors, AC, BC and AB. The students should be asked to discuss the following in their groups.
1. Why does the crease made produce the perpendicular bisector of each of the sides in ABC?
2. Where would the point O be in a right triangle?
3. If ABC is scalene, none of the perpendicular bisectors passes through a vertex. Would this be true of an isosceles triangle? an equilateral triangle?
Redirect the students attention to the beginning question. Are you able to draw a circle through the vertices of any triangle?
The teacher might then follow up with a GSP lab having the students create many triangles to test their conjectures.
CONSTRUCTION:
As shown below draw a triangle ABC and construct the perpendicular bisectors using GSP.
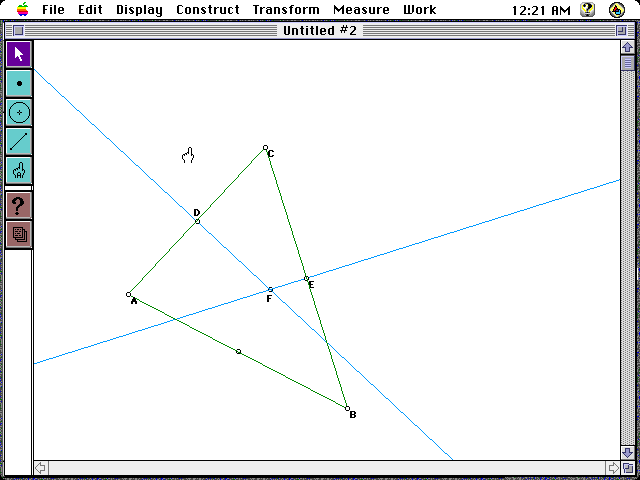
GSP LAB: Click here for a GSP sketch to explore the following questions.
Let F be the intersection of the two perpendicular bisectors. Trace it.
Observe the trace of point F as you drag point C. What do you conjecture the trace of point F is?
Measure the distance from F to other points. What relationships do you find among the distances?
Construct the object which you conjecture is the trace of point F. Check to see if F travels along the object as you move point C.
Construct the circle with center F through point C.
What do you observe? How is this exploration related to earlier investigations?
Conclusions: The circumcircle of a triangle is the circle passing through all three of the vertices of the triangle. The center of the circle is the circumcenter of the triangle.
Classroom followup: Prove that the perpendicular bisectors of the sides of a triangle are concurrent in a point this is equidistant from the three vertices of the triangle.
RETURN TO HOME PAGE