ASSIGNMENT EIGHT

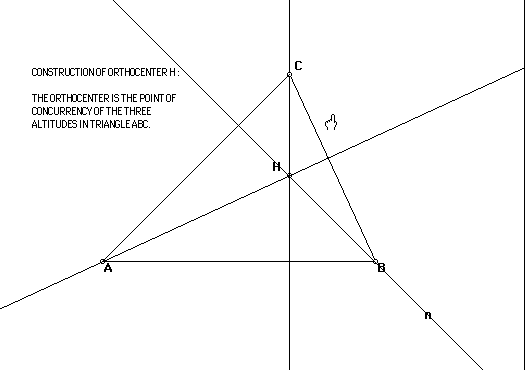
The following is a sequence of GSP drawings which explore the altitudes and orthocenters of various triangles. I began by constructing an arbitrary triangle ABC and the orthocenter of ABC which will be point H.

 



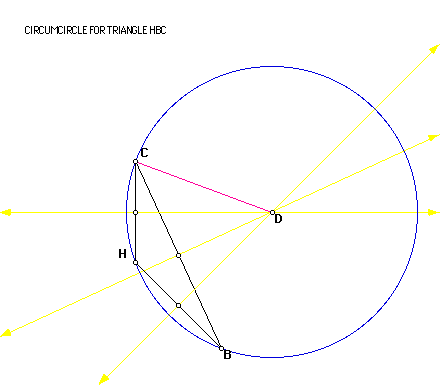
Next I will construct the orthocenter of triangle HBC.



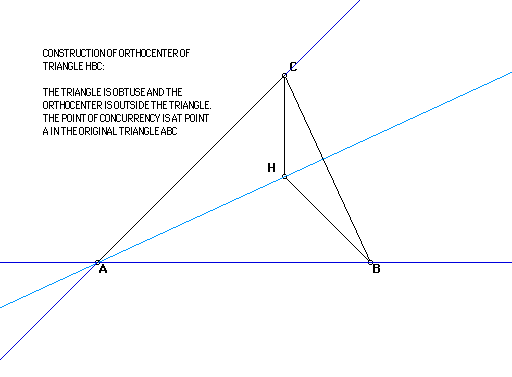
Note the point of concurrency of the three altitudes is not only exterior to the triangle HBC, but it is the point A which was in the original triangle.

Continuing I will construct the orthocenter of triangle HAB.



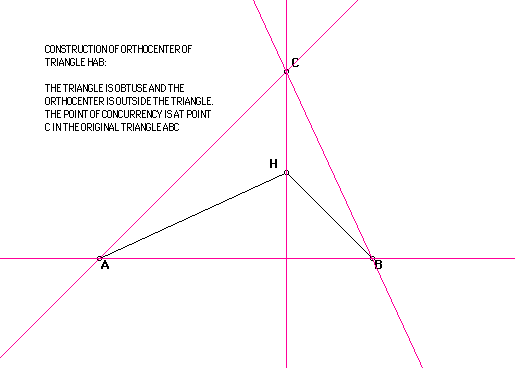
Again we observe the point of concurrency is outside the triangle and it is the point C of the original triangle. We will conjecture that the orthocenter for triangle HAC will be point B.



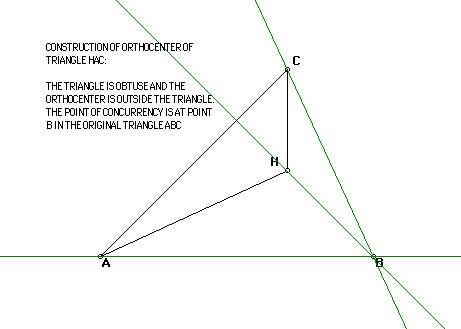
We can conclude that the lines containing the altitudes of a triangle are concurrent and follow up with a proof.



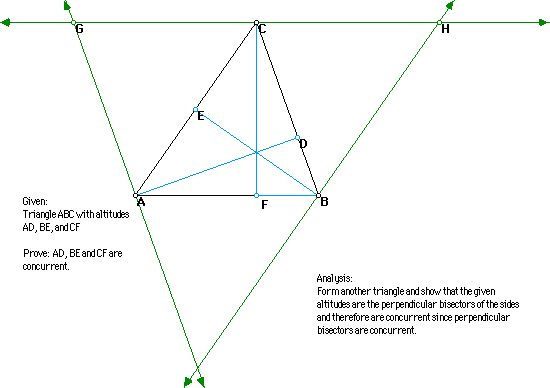
Statements

1. Triangle ABC has altitudes AD, BE and CF.

2. Through C draw GH // AB; through B draw

HI // AC; through A draw GI // BC.

3. ABCG and ABHC are parallelograms

4. Segment GC congruent to segment AB ,

and segment AB congruent to segment CH

5. Segment GC is congruent to segment CH

6. Segment CF is perpendicular to segment AB

7. Segment CF is perpendicular to segment GH

8. Line CF is the perpendicular bisector of segment GH

9. Similarly, line AD is the perpendicular bisector of segment GI, and

line BE is the perpendicular bisector of HI.

10. Lines AD, BE, and CF are concurrent.

Reasons

1. Given

2. Parallel Postulate

3. Definition of parallelogram

4. Opposite sides of a parallelogram are equal.

5. Transitive property

6. Definition of altitude

7. If a line is perpendicular to one of two // lines, it is perpendicular to the other

8. Definition of perpendicular bisector

9. Steps 3 - 8

10. The perpendicular bisectors of the sides of a triangle are concurrent.

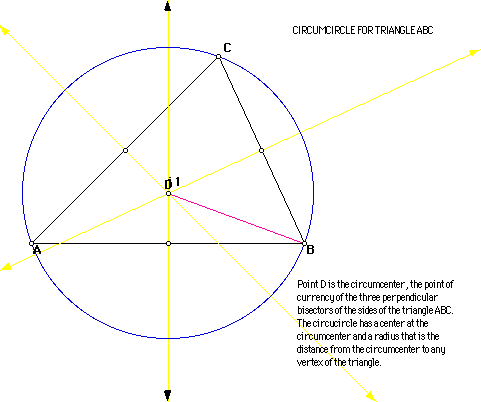
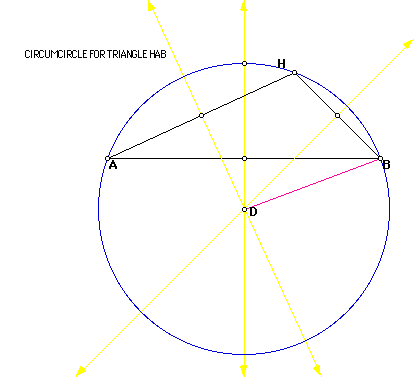
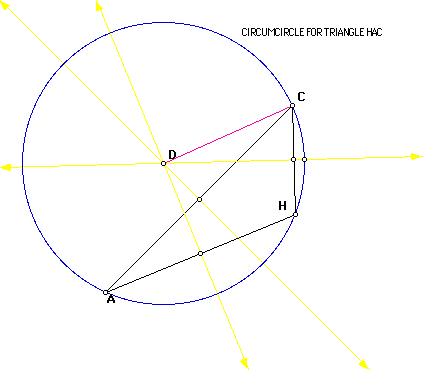
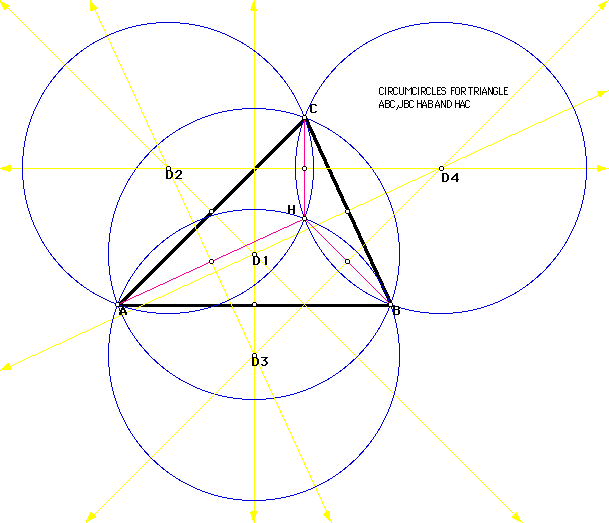
Next I will construct the circumcircles of the triangles ABC, HBC, HAB, and HAC individually and then collectively. The circumcircle is the circle that contains each of the vertices of the original triangle. It is constructed using the circumcenter which is the point of concurrency of the perpendicular bisectors of each side. The circumcenter may lie within or outside of the triangle.











 

To explore and determine whether the relationships hold for different triangles click here for a GSP sketch. Note that each of the circles go through at least two vertices of the original triangle. Students could be asked to explore special cases, right triangles, equilateral triangles and more. There are also some relationships with regard to perimeter that might be explored in a lab setting.


RETURN TO SANDY'S HOME PAGE