This investigation will focus on Pedal Triangles. Given any triangle ABC and an arbitrary point P in the plane a Pedal Triangle will be formed by constructing perpendiculars to each side of triangle ABC (extending the sides when necessary) which go through point P. Label the intersection of these perpendiculars and the sides of ABC to form a new triangle RST. Triangle RST is a Pedal Triangle for the Pedal Point P.



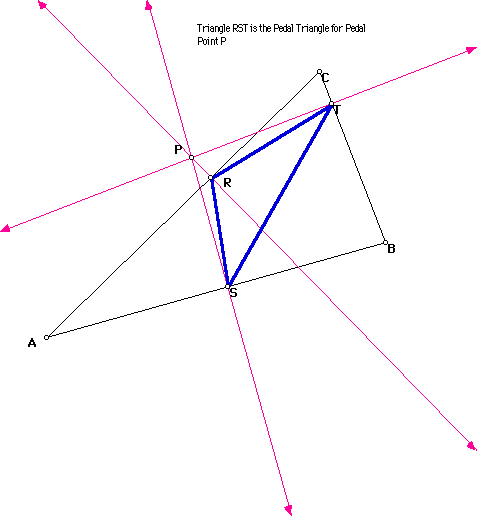
To explore more yourself click HERE to move the vertices and find various cases.

Next we will look at what will happen if the point P is the incenter of the triangle ABC.



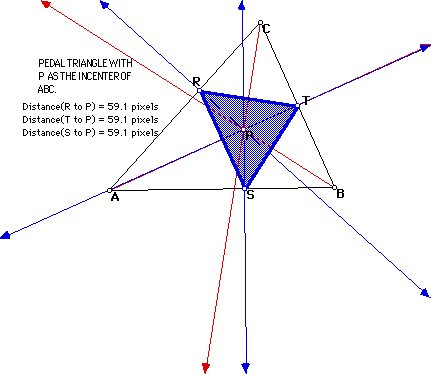
The definition of incenter is the point which is equidistant from the three sides of the triangle. It turns out that the point P which is the incenter of triangle ABC is also the circumcenter of the Pedal triangle RST.

Another special case that we might want to look at is what will happen when P is the orthocenter of the triangle ABC. We find that when P is the orthocenter of the original triangle and this triangle is not obtuse, then P will be the incenter of the Pedal Triangle. See below.



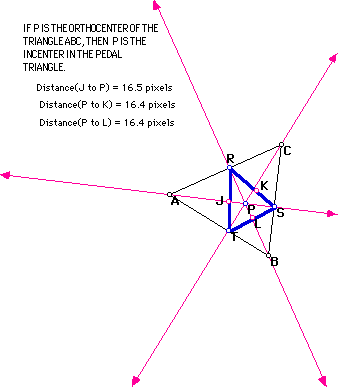
You might want to explore this for other relationships. For example notice that the vertices of the Pedal triangle all lie on the original triangle ABC. How would this change if the Pedal point were outside ABC? What happens when ABC is a right triangle? Will the Pedal Point still be the incenter for RST?



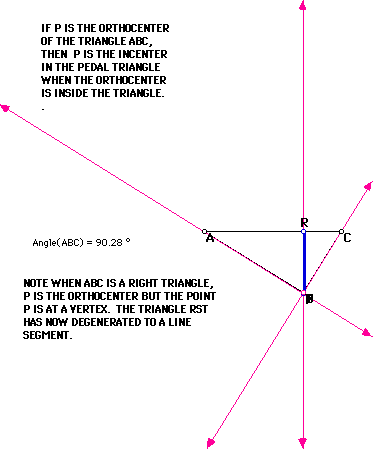
This is one condition that generates what is called the Simson Line. A Simson Line is formed when the Pedal triangle forms a line segment. In general a Simson Line will be formed when P is on a vertex of ABC. Are there other conditions? Click Here to explore.

Next we will look at when P is the centroid of ABC. Recall the centroid is the point of concurrency of all the altitudes of ABC.



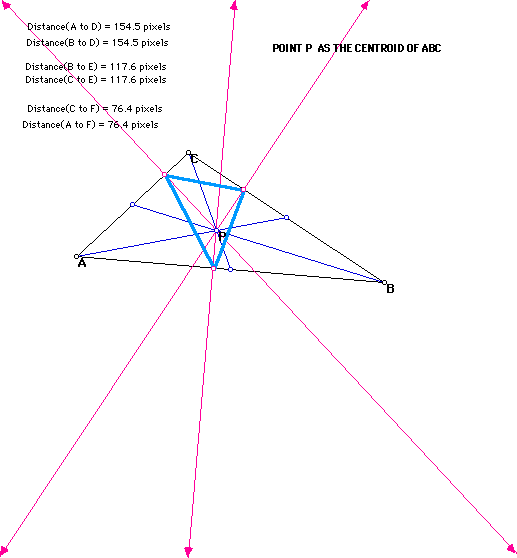
It is evident that the Pedal Triangle has its vertices on the original triangle however when we draw an obtuse triangle the Pedal Triangle again degenerates to a line. Try exploring with this sketch to see the Simson Line. Click HERE to get a sketch.

RETURN TO SANDY'S HOME PAGE.