Lori Pearman
EMT 725
Problem: Use the Arithmetic Mean -- Geometric Mean Inequality to
find the maximum volume of a box made from a 25 by 25 square sheet of cardboard
by removing a small square from each corner and folding up the sides to
form a lidless box.
Volume = V = x(25 - 2x)^2
= (1/4)(25 - 2x)(25 - 2x)(4x)
< or = (1/4) (50/3)^3 = 1157.407
This shows that the maximum volume is 1157.407 . This occurs when x = 4.167.
We can check this by graphing the above volume equation.
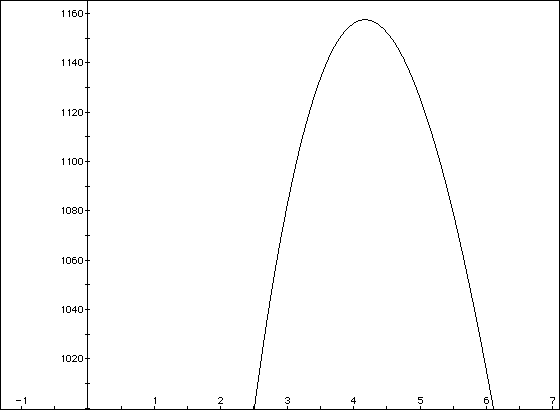
From the graph, we can see that the maximum volume is about 1157.4 and
that this occurs when x is about 4.
How could the arithmetic -- geometric mean inequality be used to determine
the shape boxes that could be created from a 25 by 25 square sheet if the
volume is 100 cu. units?
Once again, the volume equals x (25 - 2x)^2. The inequality gives:
(50 - 4x +x)/3 > or = [x(25 - 2x)^2]^(1/3). Substituting 100 in for x(25
- 2x)^2 gives:
(50 - 3x)/3 > or = 100 ^(1/3)
50 - 3x > or = (4.64)(3)
-3x > or = -36.08
x < or = 12.026666
I know this is true because the sides of the box which equal 25 - 2x should
be positive.
25 -2x > 0 implies that x < 12.5. I also know that x must be positive,
so 0 < x < 12.5.
The same things would be true for volumes of 200 and 400 cu units.
If a given volume were set equal to x(25 - 2x)^2, then one could solve for
the x value that would produce that volume. For example, 100 = x (25 - 2x)^2
implies that x = 10.99.
Now let's use the AM - GM inequality to discuss the maximum volume of
a box formed from an
n X n square sheet of cardboard.
Here, volume V = x(n - 2x)^2 = [4x(n - 2x)^2]/4
(1/4)(2n/3)^3 > or = (1/4) [4x(n - 2x)^2] = V
(1/4)(2n/3)^3 > or = x(n-2x)^2
The maximum value is (1/4)(2n/3)^3. This occurs when 4x = n - 2x, or when
x = n/6.
Now let's compare this to the maximum value we would get using calculus.
V = x(n - 2x)^2
V ' = 2(n - 2x)(-2)x + (n - 2x)^2
= -4x (n - 2x) + (n - 2x)^2 = 0
(n - 2x)[-4x + (n - 2x)] = 0
(n - 2x)(n - 6x) = 0
n - 2x = 0 or n - 6x = 0
n/2 = x or n/6 = x
x= n/2 gives a volume of 0, so the maximum volume occurs when x = n/6.
Why will the AM - GM inequality not be a useful tool when the sheet
of cardboard is 20 by 25?
Here, volume = x(20 - 2x)(25 - 2x) = (1/4) (4x)(20 - 2x)(25 - 2x)
< or = (1/4) (45/3)^3 = 843.75 for positive terms (sides).
Even though we seem to have a maximum value for the volume, there is equality
if
x = 20 - 2x = 25 - 2x. There is no x value that will satisfy these equations.
20 - 2x = 25 - 2x implies that 20 = 25 which is false.
Return to Lori's EMT 725 Page

