S. McAdams

Conic Sections

This unit of study will give definitions, examples, applications and labs that may be used with conic sections. The nonempty intersection of a plane with a cone is called a conic section. The cross sections of the cone which will be studied will include the circle, ellipse, hyperbola and parabola. The cone itself is what many would refer to as a double cone or hour glass type figure. It is possible to cut a cone so as to obtain a single point, a line or intersecting lines. This cases are called degenerate conic sections and will not be studied in this unit. In this unit we will study certain equations of second degree and their graphs.

The Circle

By definition a circle is the set of all points in a plane that are equidistant from a given point, called the center. Any segment whose endpoints are the center and a point on the circle is the radius of the circle. To develop the equation for the circle we will look at an arbitrary point (x,y) and use the definition.

Assume (x,y) is on the circle and its center is at the origin. Assume also it is a distance r from the origin.

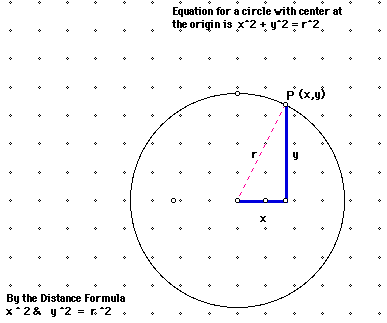
Then by the distance formula we obtain the following:

* r ^2 = ( x-0) ^2 + (y-0)^2

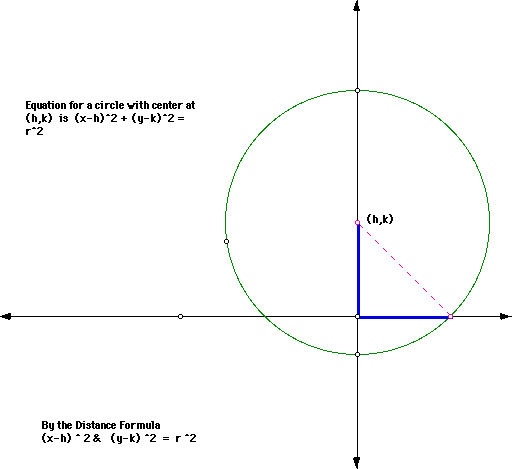
Therefore (x,y) is on the circle. Next assume x^2 + y^2 = r^2. Now this is equivalent to (x-0) ^2 + (y-0) ^2 = r^2 . By taking the principal square root we find that the distance from (x,y) to (0,0) is r, so (x,y) is on the circle. Note the student should understand that the center is not a part of the circle and (0,0) does not satisfy the circle equation. The equation * is also used in a circle with a center ( h ,k) with a few minor changes. The general equation for a circle then which center (h,k) and radius r is r ^2 = ( x-h) ^2 + (y-k)^2 . Remind students that replacing x by (x-h) and y by ( y-k) yields an equation which is the same as the original but shifted h units right and k units up.

Student objectives:

The student will be able to:

1. Find the equation for a circle given the center and radius

2. Graph the circle given the equation.

3. Write standard form for a circle using completing the square.

4. Find the equation of a circle given various conditions.

Time line:

Objectives 1 and 2 can be covered along with an introduction to conics in one day.

Objective 3 and 4 should take at least two days and possibly three. Students should be given ample time to learn completing the square. If the student is seeing this process for the first time, two instructional days would be warranted.

Obj. 1

Example: 1. Find the equation of a circle with center ( 0,0) and radius 9.

2. Find the equation of a circle with center (4,5) and radius pi.

3. Find the equation of a circle with center ( -3,-6) and radius 2.

Obj. 2

Example: Graph the circles from the equations written in the previous examples. Give several examples in which the student will have to square radicals, take the square roots of nonperfect squares and translate graphs. Also have the student give the equation from a graph. Reversibility is a useful strategy to help the teacher ascertain whether the student is confident with the concept.

Obj. 3

Example: 1. Find the center and radius for the following equations. Students will have to learn completing the square. Begin with examples which have a leading coefficient of 1. Progress to examples where the student will have to factor out the leading coefficient After ample practice continue with examples where the leading coefficient must be factored out and an odd middle coefficient remains. This will enhance the students abilities to calculate using fractions in the context of completing the square. Be certain that the student is working several examples not just watching you. The more talented the class (gifted, etc.) the less repetition they will need. It is challenging for lower level students and many repetitions will help their confidence in using fraction rules.

1.

2.

3.

4.

Obj. 4

Students should be given problems in which they are given only a part of the needed information to write a circle equation. Drawing diagrams will be an aid to the student when solving these problems. Some examples follow:

Example:

1. Find the equation for a circle with a center at ( -4,3) which is tangent to the x axis.

2. Find an equation for a circle for which the endpoints of the diameter are ( 5, -3) and (-3, 7)

3. Determine whether the point is a point on the unit circle.

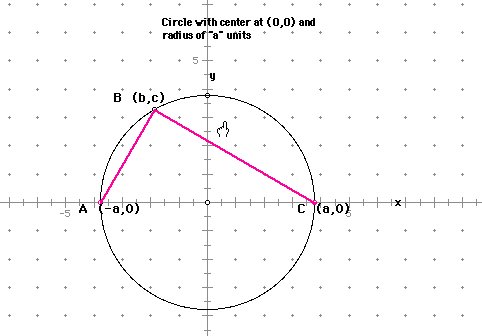
4. Prove that angle ABC is a right angle. Assume point B is on the circle whose radius is a, and whose center is at the origin. See diagram or require the students to draw one.

5. Sketch the circles . Find the intersection points of the circles. Find the equation for the line containing their common chord.

The circle may always be introduced with the ellipse as a special case. It should be noted that the coefficients of the squared terms in a circle are equal. This is a distinquishing factor when students try to determine which conic they are observing after all of the conic sections have been introduced.

Assessment:

Write an equation for a circle given the following information:

1. The center is at ( -3, 2) and the radius is .

2. The center is ( a,b) and the radius is r.

3. The center is (1,3) and the circle passes through the point (4,7).

4. The center is in the second quadrant, the radius is 6, and the circle is tangent to both axes.

5. The center is ( 7, -3) and the circle is tangent to the line y = 2.

Rewrite each equation in standard form.

6.

7.

8.

9.

10. Graph the circle in question 1.

11. Graph the circle in question 5.

Click here to return to Instuctional Unit for more conics.