S. McAdams
RELATED TOPICS
There are a variety of related topics that one could discuss while discussing the conic sections. The following are few examples that might be used as a spring board to other discusssions. The discussions below include polar coordinates, parametric equations, systems of equations and applications of systems of equations.
When studying circles it would be appropriate to introduce a few of the concepts found in circle trigonometry. For example one extention might include the discussion of polor coordinates and trigonometric functions.
Polar Coordinates:
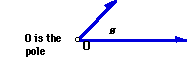
An equation for a curve given in terms of r and ø is called a polar equation. When first exploring polar equations is it helpful to graph by hand using polar coordinates to obtain a understanding of why the curve appears as it does. Like Cartesian coordinates polar coordinates have two values, Theta (ø) and r. Theta is the measure of the angle in standard position measured counterclockwise from the polar axis, and r is the directed distance from the pole to the point P in the plane. Polar coordinates use both a distance from a reference point and an angle to describe locations. The position of a point P in the plane can be described by giving its distance r from a point O called the pole. (See diagram below)
It is customary to let the pole coincide with the origin in a Cartesian coordinate system, and to let the polar axis coincide with the positive x axis. The typical notation for polar coordinates is (r; ø), however, ø is the independent variable.
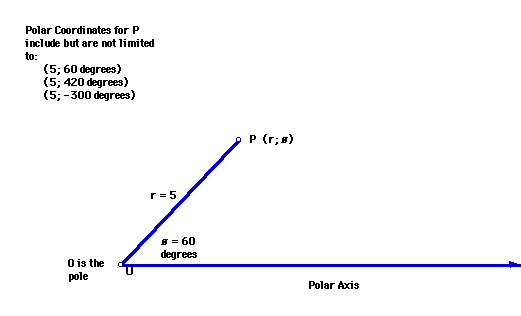
When working with polar coordinates angles do not have to have values between 0 degrees and 360 degrees. A single point may have many pairs of polar coordinates since there can be an infinite number of coterminal angles passing through any given point. If we use the same value for r and find a value of ø + 360 n for any integer value of n we will be able to locate a coterminal angle for ø. For example the diagram below can indicate any of the following polar coordinates and many others as well.
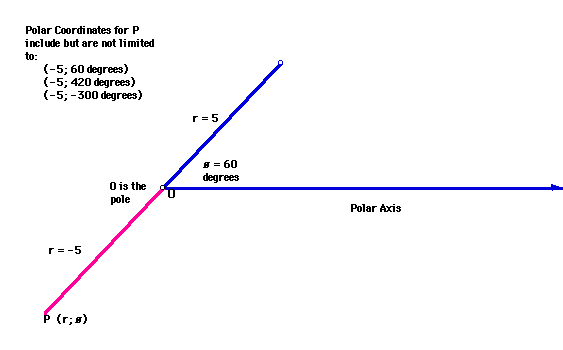
Since r is a directed distance r can be a negative number. If r is a negative number the point (r;ø) is plotted as ( | r | ; ø + pi). That is if r < 0 measure the angle ø as usual, then go in the opposite direction from the ray normally drawn. See an example below.
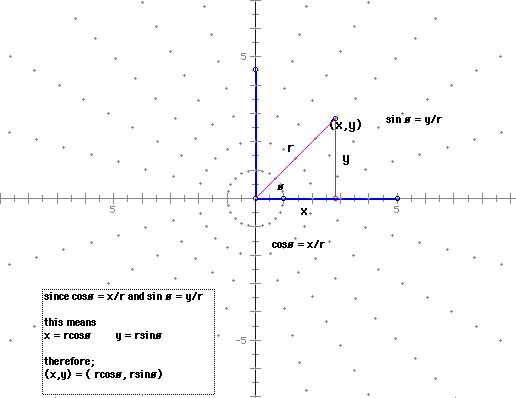
It is recommended that students practice graphing polar coordinates on polar graph paper to familiarize themselves with how the curve is formed. Students will need practice converting from rectangular coordinates to polar coordinates. Example: Convert ( 38 , 82 degrees) to rectangular coordinates. The student will need to understand the relationship between the x y plane and how it relates to the r ø plane. The basic trigonometric functions sine and cosine could be reviewed or discussed, then have students draw a diagram to show the relationship between (x,y) and (rcosø, rsinø).
To continue with the example (38 cos 82 degrees, 38 sin 82 degrees) would give rectangular coordinates of approximately ( 5.3, 37.6 degrees) Of course many calculators convert readily between the two coordinate systems, but students will not have an understanding of how the values are being derived without drawing and reasoning through several graphing examples.
After a basic understanding of polar coordinates is reached a lab might include locating polar coordinates on a map. How could students find polar coordinates on a map that did not contain a polar grid? Simply have them measure distances using a ruler or compass and measure angles using a protractor.You would begin by designating a reference point. Other lab ideas include using maps of constellations and astronomy applications. Also students enjoy creating their own maps to locate a hidden treasure outside the classroom. This is a great warm weather activitiy that allows the students to move about and apply the concepts literally. Another extention could include the concept of bearing and many students in scouts have learned something about orienteering which makes a good outside activity as well.
This dialog on polar coordinates could be very limited or it could launch into a full discussion of the unit circle and circle trignometry if that is the direction in which the teacher plans to go.
To further explore circles we will look at parametric curves. The word parameter means a variable used to describe the general form of a set of equations. The two equations give the x and y coordinates of a moving object at time t. The two equations are called a set or pair of parametric equations of the curve and the variable t is called the parameter.
Students could begin their discovery by making a chart of values and plotting the points for the x,y pairs. Or with the technology available the teacher might begin by graphing various parametric equations and allowing the students to discover the relationship.
Objectives:
1. Students will be able to graph parametric equations of circles.
2. Students will be able to combine two parametric equations into a single equation.
Example:
Suppose an object's motion is described by the parametric equations:
x = 2 cosø y = 2 sinø
1. Graph to plot the path of this object.
2. Next combine the two equations to form one equation.
Solution:
The equation graphs as a circle with center (0,0) and radius = 2
Solve for cosø and sinø in the given parametric equations.
cosø = x/2 and sinø = y/2. Using the Pythagorean Identity :
therefore, 
which indicates 
which can be written
as 
. The students
will recognize this as a circle, center ( 0,0) and radius = 2.
This could be followed by a lab on parametrics of the formx = a cos ø +b and y = a sinø + c.
This could naturally lead into the equation for an ellipse.
Example: x = 6 cos ø + 3 and y = 6 sin ø -1. Students will graph a circle with center ( -3,1) and a radius of 6. They will naturally want to know what happens when the "a" term is not the same for the x and y coordinates. This could lead into a nice introduction of the ellipse.
After learning to graph each of the conic sections students could be introduced to systems with conics. The following lab introduces the student to the idea of using the discriminant to determine the type of conic. Using MacNumerics or the TI 81, 82, 83 or 85 a student can locate the points of intersection of a line and a conic or two conics to determine the solution. It would also be good practice with algebra skills to show them how to solve these systems algebraically.
Objectives: Use the discriminant to determine the shape of the conic section. Sketch the graph of each conic given. Find the points of intersection to determine the solution(s) for the system.
The general form of a conic section is 
. The introduction
of the xy term complicates how one determines the shape of the conic. If
the conic is not degenerate the following rules will apply:
1. If 
the conic is
an ellipse.
2. If 
the conic is
a parabola
3. If 
the conic is
an hyperbola.
For each of the following conic sections :
A. Find the discriminant and predict the shape of the conic.
B. Sketch the graph using MacNumerics, Conics.
1. 
2. 
3.
4. 
Graph the following conics by hand.
5.
6. 
The following are examples of systems of conics. The student may be required to graph the conics by hand and estimate the intersection points or one might require them to use a calculator to graph some of the examples and use the intersect feature on the calculator. The draw back for using the graphing calculators however is that many calculators will only graph functions. One of the best tools for solving systems can be found on the computer. There are various software packages that allow the conics to be graphed. In particular MacNumerics can be used to demonstrate these concepts. There is some value in requiring students verify at least a few solutions algebraically. The following are some sample systems that could be used. Some use linear functions with conics, others include only conics. Solving linear and conic systems is good practice for the substitution method. Solving conic systems usually involves linear combinations, although if a parabola is involved substitution may still be the method of choice.
Solve the following systems.
1.
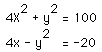
2. 
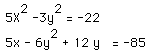
3. 
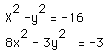
4. 
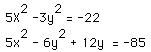
There are various applications of conic systems. Following is one such problem taken from a precalculus book written by Forrester.
Objective: The student will use MacNumerics or other computer software to graph systems and interpret solutions. Alternately the student will be able to solve a system of conics algebraically.
Suppose that you have been hired by the Palomar Observatory near San
Diego. Your assignment is to track incoming meteorites to find out whether
or not they will strike the earth. Since the earth has a circular cross
section, you decide to set up a Cartesian coordinate system with its origin
at the center of the earth. The equation of the earth's surface is 
where x and y are distances in thousands of kilometers.
A. The first meteorite you observe is moving along the parabola whose
equation is 
. Will this meteorite strike the earth's surface?
If so, where? If not, how can you tell?
B. The second meteorite is coming in from the lower left along one branch
of the hyperbola
(see sketch) Will it strike the earth's surface?
If so, where? If not, how can you tell?
C. To the nearest 100 kilometers, what is the radius of the earth?
This particular question can be a part of several applications that could be solved using MacNumerics in a computer lab on applications.
Solution:
A. The first meteorite will miss the earth. There is no intersection for these two equations as is evident in the following diagram taken from MacNumerics.
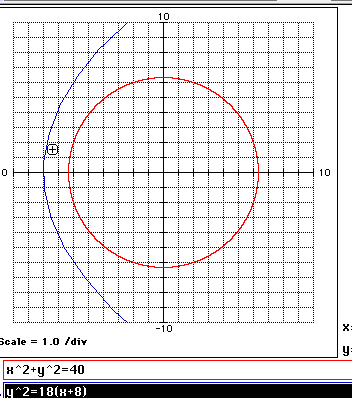
The teacher may ask the students to show algebraically why this system has no solution.
B. This meteorite will strike the earth. See below.
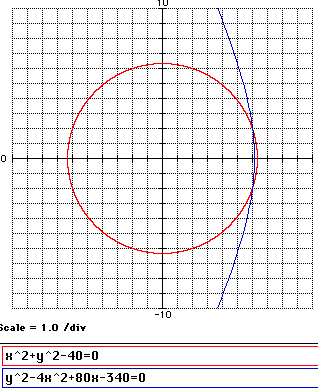
Using MacNumerics the intersection occurs at (6, -2). The teacher may want the students to solve this algebraically or at least indicate how they know that this solution is accurate.
CLICK HERE TO RETURN TO INSTRUCTIONAL UNIT PAGE