
Objectives:
The Parabola is defined as "the set of all points P in a plane equidistant from a fixed line and a fixed point in the plane." The fixed line is called the directrix, and the fixed point is called the focus.
A parabola, as shown on the cables of the Golden Gate Bridge (below), can be seen in many different forms. The path that a thrown ball takes or the flow of water from a hose each illustrate the shape of the parabola.

Each parabola is, in some form, a graph of a second-degree function and has many properties that are worthy of examination. Let's begin by looking at the standard form for the equation of a parabola.
The standard form is (x - h)2 = 4p (y - k), where the focus is (h, k + p) and the directrix is y = k - p. If the parabola is rotated so that its vertex is (h,k) and its axis of symmetry is parallel to the x-axis, it has an equation of (y - k)2 = 4p (x - h), where the focus is (h + p, k) and the directrix is x = h - p.
It would also be in our best interest to cover another form that the
equation of a parabola may appear as
y = (x - h)2 + k, where h represents the distance that the parabola
has been translated along the x axis, and k represents the distance the
parabola has been shifted up and down the y-axis.
Completing the square to get the standard form of a parabola.
We should now determine how we will arrive at an equation in the form y = (x - h)2 + k;
Example 1
Suppose we are given an equation like
y = 3x2 + 12x + 1.
We now need to complete the square for this equation. I will assume that you have had some instruction on completing the square; but in case you haven't, I will go through one example and leave the rest to the reader.
When completing the square, we first have to isolate the Ax2 term and the By term from the C term. So the first couple of steps will only deal with the first two parts of the trinomial.
In order to complete the square, the quadratic in the form y = Ax2 + By + C cannot have an A term that is anything other than 1. In our example, A = 3; so we now need to divide the 3 out, but that is only out of the 3x2 + 12x terms.
This simplifies to y = 3(x2 + 4x) + 1. From here we need to take 1/2 of our B term, then square the product. So in this case, we have 1/2(4) = 2, then 22 is 4. Now, take that 4 and place it inside the parenthetical term.
To update what we have: y = 3(x2 + 4x + 4) + 1; but we now need to keep in mind that we have added a term to our equation that must be accounted for. By adding 4 to the inside of the parenthesis, we have done more than just add 4 to the equation. We have now added 4 times the 3 that is sitting in front of the parenthetical term. So, really we are adding 12 to the equation, and we must now offset that on the same side of the equation. We will now offset by subtracting 12 from that 1 we left off to the right hand side.
To update: y = 3(x2 + 4x + 4) + 1 - 12. We have now successfully completed the square. Now we need to get this into more friendly terms. The inside of the parenthesis (the completed square) can be simplified to (x + 2)2. The final version after the smoke clears is y = 3(x + 2)2 - 11. And , oh the wealth of information we can pull from something like this! We will find the specifics from this type of equation below.
Finding the vertex, line of symmetry, and maximum and minimum value for the defined quadratic function.
Let's first focus on the second form mentioned, y =(x - h)2 + k. When we have an equation in this form, we can safely say that the 'h' represents the same thing that 'h' represented in the first standard form that we mentioned, as does the 'k'. When we have an equation like y = (x - 3)2 + 4, we see that the graph has been shifted 3 units to the right and 4 units upward. The picture below shows this parabola in the first quadrant.
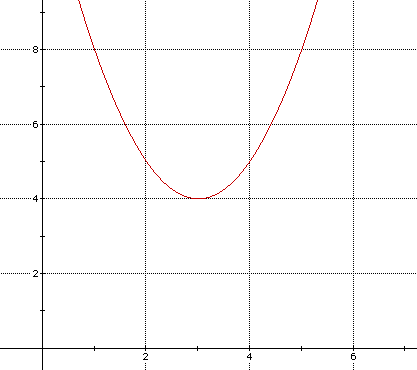
Had the inside of the parenthesis in the example equation read,"(x+3)" as opposed to "(x-3)," then the graph would have been shifted three units to the left of the origin. The "+4" at the end of the equation tells the graph to shift up four units. Likewise, had the equation read "-4," then the graph would still be pointed upward, but the vertex would have been four units below the x-axis.
A great deal can be determined by an equation in this form.
The most obvious thing that we can tell, without having to look at the graph, is the origin. The origin can be found by pairing the h value with the k value, to give the coordinate (h, k). The most obvious mistake that can arise from this is by taking the wrong sign of the 'h.' In our example equation, y = (x - 3)2 + 4, we noticed that the 'h' is 3, but it is often mistaken that the x-coordinate of our vertex is -3; this is not the case because our standard form for the equation is y = (x - h)2 + k, implying that the we need to change the sign of what is inside the parenthesis.
To find the line of symmetry of a parabola in this form, we need to remember that we are only dealing with parabolas that are pointed up or down in nature. With this in mind, the line of symmetry (also known as the axis of symmetry) is the line that splits the parabola into two separate branches that mirror each other. The line of symmetry goes through the vertex, and since we are now only dealing with parabolas that go up and down, the line of symmetry must be a vertical line that will begin with "x = _ ". The number that goes in this blank will be the x-coordinate of the vertex. For example, when we looked at y = (x - 3)2 + 4, the x-coordinate of the vertex is going be 3; so the equation for the line of symmetry is x = 3.
In order to visualize the line of symmetry, take the picture of the parabola above and draw an imaginary vertical line through the vertex. If you were to take the equation of that vertical line, you would notice that the line is going through the x-axis at x = 3. An easy mistake that students often make is that they say that the line of symmetry is y = 3 since the line is vertical. We must keep in mind that the equations for vertical and horizontal lines are the reverse of what you expect them to be. We always say that vertical means "up and down; so the equation of the line (being parallel to the y-axis) begins with 'y =__'," but we forget that the key is which axis the line goes through. So since the line goes through the x-axis, the equation for this vertical line must be x = __.
In the line of symmetry discussion, we dealt with the x-coordinate of the vertex; and just like clockwork, we need to now examine the y-coordinate. The y-coordinate of the vertex tells us how high or how low the parabola sits.
Once again with our trusty example, y = (x-3)2 + 4, we see that the y-coordinate of the vertex (as derived from the number on the far right of the equation) dictates how high or low on the coordinate plane that the parabola sits. This parabola is resting on the line y = 4 (see line of symmetry for why the equation is y = __, instead of x = __ ). Once we have identified what the y-coordinate is, the last question we have is whether this number represents a maximum or minimum. We call this number a maximum if the parabola is facing downward (the vertex represents the highest point on the parabola), and we can call it a minimum if the parabola is facing upward (the vertex represents the lowest point on the parabola).
How do we tell if the parabola is pointed upward or downward by just looking at the equation?
As long as we have the equation in the form derived from the completing the square step, we look and see if there is a negative sign in front of the parenthetical term. If the equation comes in the form of y = - (x - h)2 + k, the negative in front of the parenthesis tells us that the parabola is pointed downward (as illustrated in the picture below). If there is no negative sign in front, then the parabola faces upward.
Example 2
Let's now look at an example of another equation of a parabola in standard form. We will then identify its vertex, line of symmetry, and maximum or minimum.
For example, let's take the equation y = - (x + 4)2 - 7. The first thing we would like to do is look at the graph of the curve. This should help us make sense of the things we are looking for. The graph is shown below.
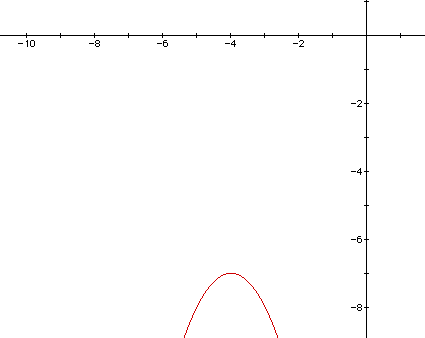
As you can see, this curve falls into the third quadrant and is pointed downward. The vertex appears to have a negative x-coordinate and a negative y-coordinate. We will look more closely at the equation and take what we have already learned, we should be satisfied with our results.
y = - (x + 4)2 - 7 gives us a vertex of (-4, -7). The x-coordinate is the "opposite" of 4, which is -4, and the y-coordinate is -7 as seen from the number that sits at the end of the equation.
First, the negative sign at the beginning of the equation immediately tips us off that the parabola is facing downward.
Next, the x-coordinate that we found is the key to finding the line of symmetry. We know that the equation for the line of symmetry will be "x = __ ," and the number inside the blank is the x-coordinate, -4.
Lastly, we need to decide whether we have a maximum or minimum. The y-coordinate is going to be a maximum in this case because the vertex lies on the highest point (maximum) of our curve. So in this case, we have a maximum of y = -7.
Let's now look at the same curve above with the vertex, line of symmetry, and maximum visible:
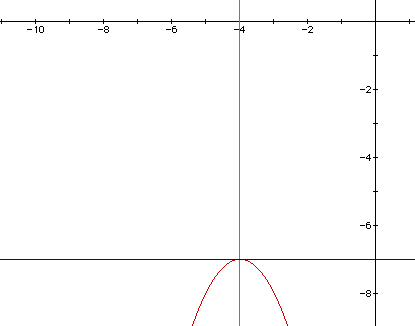
Obviously, the red curve represents the parabola. The green line represents our line of symmetry (equation x = -4) and the blue line represents the line that the maximum rests on at y = -7. Hopefully this visual has helped you see all of the specific parts that we have discussed so far.
For some supplementary exercises over what we have covered so far click here: Exercise 1
Find the vertex, focus, and directrix, and draw a graph of a parabola, given its equation.
As you may or may not know, a parabola is the locus of points in a plane equidistant from a fixed line and a fixed point on the plane. We know this fixed line to be the directrix and the fixed point to be the focus.
To see an animated picture of the above description, you need to have Geometer's SketchPad for either Macintosh or PC loaded on your computer. If you have GSP, click here. To download the script of this picture so you can create it yourself, click here.
Let's now take a look at a parabola that has all of the elements that we will be looking for:
The following example is especially meant for those who do not have GSP on your computer. This picture (below) is generated from Algebra Xpresser.
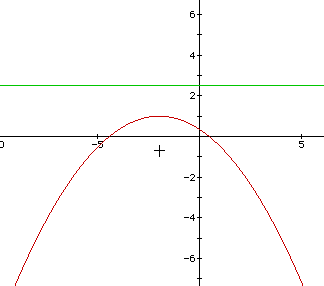
From the above picture, I have labeled three items that we need to pay close attention to. The highest point of the parabola is the vertex (and the maximum). The plus sign that is directly under the vertex is the focus. The green line that is above the parabola (and directly above the vertex) is the directrix. You may be able to see, by eyeballing, that the distance from the focus to the vertex is the same distance as the vertex to the directrix. We will now go into a bit of detail as to how to derive all of this information from a given equation.
The next example that I will give you will be a nice, easy equation from which we can easily pick the information we need.
Example 3
Let's examine the equation, (x + 2)2 = -6(y - 1).
Obviously, this equation is different from the "vertex form" we learned in the prior lesson. Even still we can find all of the information we found in the first lesson: the vertex, line of symmetry, and the maximum/minimum. We have to apply the same line of thought that the vertex is where the x and y terms are. In the same manner we find the x-coordinate is -2, the y-coordinate is 1 {V: (-2, 1)}. All we need to find the line of symmetry and the maximum/minimum is the vertex; so let's follow through: The line of symmetry is x = -2, and the maximum (since we have a negative sign in front of one of our terms) is at y = 1.
Now for the fun part.
In order to find the focus and directrix of the parabola, we need to have the equations that give an up or down facing parabola in the form (x - h)2 = 4p(y - k) form. In other words, we need to have the x2 term isolated from the rest of the equation. We are used to having x2 by itself, but if the vertex has been shifted either up or down, we need to show this in the parenthetical term with the y. The coefficient of the (y - k) term is the 4p term. We need to take this number and set it equal to 4p.
In this case, 4p is equal to the term in front of the y term (in parenthesis); so 4p = -6. This means that p = -3/2. Since this is an downward facing parabola, we need to have the focus inside of the curve, meaning the focus is below the vertex. How far below the vertex? Take the y-coordinate and add the p term it. So, we now have the vertex at (-2, 1) and we are, in essence, subtracting -3/2 from 1. This will move the focus to the point (-2, -1/2).
The directrix is equidistant from the vertex that the focus is. So if the focus is down -3/2 from the vertex, then the directrix is a line that is up 3/2 from the vertex. That puts the directrix at y = 5/2.
For an illustration of this problem, please look at the picture below:
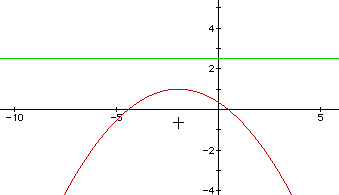
The green line (3/2 units up from the vertex) is the directrix, and the plus sign 3/2 units down from the vertex is the focus.
This should help us with the parabolas that open upward and downward. Let's now take a look at a parabolat that opens left and right.
Example 4
Let's take a look at the equation (y + 3)2= 12 (x - 1).
We can easily identify that the parabola is opening left or right. Since the coefficient in front of the x term is positive, we can say that the parabola will open to the right. The focus will be to the right of the vertex, and the directrix will be a vertical line that is the same distance to the left of the vertex that the focus is to the right.
The vertex is (1, -3), the axis of symmetry (now horizontal) is y = -3, and we don't recognize "max's and min's" for parabolas that open left or right.
The term in front of the x term is a 12. This is what our 4p term is equal to. So 4p = 12, making p = 3. So we now need to move the focus 3 units right from the the origin. This means that the coordinate for the focus is (4, -3), and the directrix will be a vertical line going through the point (-2, -3).
This problem is illustrated in the picture below.
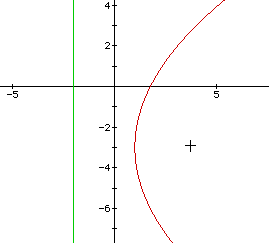
Once again, our green line represents the directrix and the plus sign represents the aforementioned focus.
For some supplementary exercises over what we have covered in lesson 2, click here: Exercise 2
Find the equation of a parabola when we are given the coordinates of its focus and vertex.
Now, we are going to begin taking what we have learned and start piecing it together. If we are given a focus and a vertex, we have enough to be able to generate a quadratic equation of a parabola. If we think about it for a second, we will be able to find the distance from the vertex to the focus based on this given information. We will then be able to calculate our p term (the term from the previous lesson that is in front of our non-squared variable). Placing the coordinates of the vertex into the equation is very simple, relative to what we have learned so far.
Example 5
Let us suppose that we are given a focus of (-6, 0) and the vertex is at the origin.
Based on what we know without plugging anything in, we can say that the parabola will be opening up to the left because its focus is to the left of the origin. Now in beginning to piece things together, we can say that the equation will be something like y2 is equal to some x term.
Since the origin is the vertex, we can say that this will be (y - 0)2 = 4p(x - 0), which simplifies to y2 = 4px.
We know that p = -6, and we know that 4p = -24. We should now be able to tell that the equation is y2 = -24x.
Example 6
We will now try a problem that has the parabola opening up or down. We will make the focus (2, 3) and the vertex (2, 6).
The focus is directly below the vertex by 3 units; so p = -3; so 4p = -12; but not so fast! We aren't quite home free yet. The vertex is shifted off of the origin, and we need to consider the h and k terms.
The equation with a parabola facing downward will be (x - h)2
= 4p(y - k), where 4p is negative. To again piece things together:
(x - 2)2 = -12 (y - 2).
For some supplementary exercises over what we have covered in lesson 3, click here: Exercise 3
Find the vertex, focus, and directrix, and graph a parabola by first completing the square.
Not always do we come up on equations that are there just waiting for us to solve them. Sometimes we've got to work a bit to find their key points. Hopefully this example will lead us toward such a problem.
Example 7
The last pair of examples that we will examine will be one where we are
given a quadratic equation that is not already in any particular standard
form.
We will now be forced to complete the square to arrive at the form we need
to find the newest parts of the parabola that we have explored.
Suppose that we have x2 + 6x +4y + 5 = 0. Since the x-term is the squared term, we will choose to isolate all of the terms that have x in them. We will need to place the x terms on one side of the equation, while the rest of the terms are on the opposite side.
This step will leave us with x2 + 6x = -4y - 5. When we complete the square on the left-hand side of the equation, we will have x2 + 6x + 9; sowe will need to add 9 to the right-hand side, as well.
This will bring us to (x + 3)2 = -4y + 4. Remembering that any coefficients of the x or y terms need to go in front of the non-squared variable, we will factor the -4 from the y-term. This will leave us with (x + 3)2 = -4 (y - 1).
From here, the problem resembles both of the others.
Our vertex is (-3, 1), our line of symmetry is x = -3; and we do have a maximum at y = 1;
The focus can now be found by taking the number in front of the non-squared variable -4 and setting it equal to 4p. 4p = -4; so p = -1.
Since the parabola is facing downward, the focus is below the vertex, and the directrix is above. We will take our vertex and add (-1) to the y-coordinate. This will take us to the point (-3, 0) that is our focus. The directrix (on the opposite side of the vertex) is at the horizontal line y = 2. Once again, we will look at an illustration below. The green line is the directrix, and blue dot is the focus.
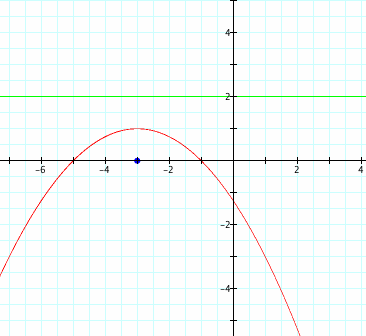
(Corrections by J. Wilson, 28 Feb 2012)
Example 8
Suppose that we have an equation y2 + 2y + 4x -8 = 0. Before we doing any steps, such as completing the square, we can see that the squared term is the y term. This will tell us that the parabola with either open to the left or to the right. Since this is the case where the y term is squared, we need to isolate the y terms to one side of the equation and put the x terms and the constants on the other. We will stick to what we've been doing all along and put the isolated terms on the left.
After the isolation step, we see that we have y2 + 2y = -4x + 8.
In completing the square, we will have y + 2y + 1 = -4x + 8 + 1; this simplifies to (y + 1)2 = -4x + 9.
No matter how ugly the right-hand side of the equation may get, we need to divide the right hand side by the coefficient of the x term (in this case, -4). This will leave us with (y + 1)2 = -4(x - 9/4). From here we can say that the parabola will open to the left.
We can now see that the vertex will be at (9/4, -1).
The term in front of the x is a -4. This is our 4p value. So we now can say that 4p = -4. In turn, our p = -1.
Now will we determine that the focus is one unit left of the vertex; so the focus (after some work with fractions) is (5/4, -1).
The directrix is going to be a vertical line that is one unit to the right of the vertex. So the directrix will be a line, x = 13/4.
Below, we will see the sketch of this equation.
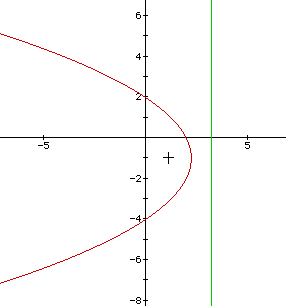
As has been the case so far, the plus sign represents the focus, which resides at the point (5/4, -1); the directrix is represented by the green line, which is on the equation x = 13/4.
For some supplementary exercises over what we have covered in lesson 4, click here: Exercise 4