

Find the ratio of the area of the region of points closer to the centroid than to the sides of an equilateral triangle to the area of the triangle.
Analysis:
Consider each side as a directrix and the Centoid as a focal point. The set of points equidistant from the centroid and the respective side would be a parabola. So the region whose area is needed to compare to the area of the triangle is the intersection of three parabolas.
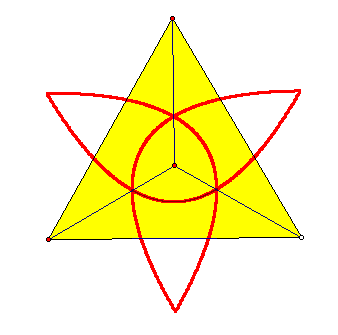
The region is shown here:

The segments from the centroid to the vertices divide the equilateral triangle into three congruent areas. Therefore, the desired ratio of the region to the equilateral triangle is the same as the region of triangle AGC that is above the arc of the parabola to the area of triangle AGC
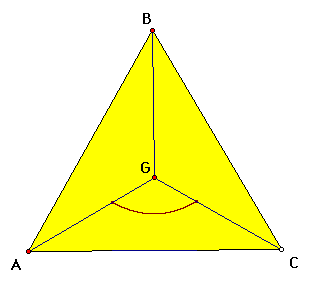
The problem is replaced by one of determining the ratio of the area of the region cut off by a parabola determined by a directrix along one side and having its focus as the vertex of the triangle.
The region cut off by the parabola can be seen as the sum of two areas, one a similar triangle and the other a section of the parabola cut off by a chord.
Achimedes, in his Quadrature of the Parabolic Section, provided us with a formula for the Quadrature of the Parabolic Section as
where a(ABC) is the area of triangle ABC. A and C are the endpoints of the chord of the parabola and B is its vertex. Erbas provides an explanation and derivation of the Archimedes quadrature.