Maximum Cylinder that can be Inscribed in a Sphere

One Solution:

Using the AM-GM inequality, what is the maximum volume of a right circular cylinder that can be inscribed in a sphere of radius R.

 

 

We can argue easily that such a cylinder exists.

 

Take a cross-section of the sphere and the inscribed cylinder through the center of the sphere. Let r be the radius of the cylinder and h its height.

 

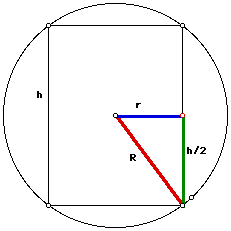
The volume is given by

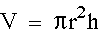
and we have the Pythagorean relationship

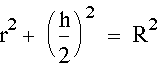
We can solve for h to get

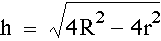
Now,

Using the AM-GM inequality

With equality if and only if

 

This gives

So the volume is always less than or equal to a constant and it can reach that constant, the maximum volume, if and only if

We have

and this happens when

Note that

 

Return