PROBLEM SOLVING WITH HERON'S FORMULA


by

James W. Wilson
University of Georgia

 

Introduction

Heron's formula for the area of a triangle with sides of length a, b, c is

where


It is unfortunate that this topic has essentially disappeared from school curriculum today. Calculation, given available calculations and computers, can no longer be a reason for avoiding the formula. In what follows, I hope to show some interesting and challenging problems using Heron's formula.

Whether or not one would pose the demonstration or proof of Heron's formula for a particular class would depend on the class. Initially, exploration with Heron's formula could involve computing areas using the formula and making comparison's of the results -- much as we pose analogous exercises in a meaningful way with the Pythagorean theorem long before a proof or demonstration is fully understood.

For instance, one exercise could be to have students measure the sides and an altitude on several triangles and, with calculator, compute the areas with both formulas



Comparison of the results could well lead to intuitions about the areas of triangles and understanding of when one formula would be more applicable than the other.

 

Heron's Formula

The demonstration and proof of Heron's formula can be done from elementary consideration of geometry and algebra. I will present an algebraic proof here.  Alternative proofs and derivations are suggested on the Jwilson web site, Heron's Formula  and a particularly concise geometric proof is given at Heron's Formula, Geometric Proof.

I  will assume the Pythagorean theorem and the area formula for a triangle

where b is the length of a base and h is the height to that base.


We have

so, for future reference,

2s = a + b + c
2(s - a) = - a + b + c
2(s - b) = a - b + c
2(s - c) = a + b - c

There is at least one side of our triangle for which the altitude lies "inside" the triangle. For convenience make that the side of length c. It will not make any difference, just simpler.



Let p + q = c as indicated. Then

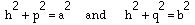
This demonstration of Heron's formula is straightforward and elementary. Working through it with students can provide fruitful ideas of strategy, symmetry, planning, and observation. We now switch to consider some problems and investigations for which Heron's formula is useful.

 

Problem:

Show that the maximum area of a triangular region with a fixed perimeter occurs for an equilateral triangle.

Comment. I would adapt the statement and context of this problem depending on the background of the students. Above, I mentioned an exploratory investigation where students looked at different triangular regions that could be formed with a perimeter of 100 feet. Now extend this. Have students organize a table where the lengths of the sides are varied systematically .

In order to vary something "systematically" one needs to identify a variable that can be ordered in the table. For example, investigate the more manageable problem of isosceles triangles. Let the side of length a be the base to vary from 2 to 48 in steps of 2, as follows

This table can be generated with a calculator in only a few minutes and the data open up lots of opportunity for discussion, plausible reasoning, and problem posing.

 

 

 


Let us return now to showing that the equilateral triangle has the most area for any fixed perimeter.

and equality occurs when s - a = s - b = s - c, that is, a = b = c. Since the product is always less than this constant, this constant is the maximum for the product and the maximum area of a triangle with a fixed perimeter 2s is

The equilateral triangle has that maximum area. For instance, the maximum area for all triangles having a perimeter of 100 is

Problem:

Interpret the condition

             s(s - c) = (s - a)(s - b)

What can be concluded for any triang

le for which the condition holds?

Investigations:

Return