Extend OP each direction to obtain a diameter of the circle.

The distance from P along this diameter to the nearest intersection with the circle is 1 - x and the distance to the other end is 1 + x.

From geometry, the products of the parts of two intersecting chords are equal, so

(PC)(PB) = (1 - x)(1 + x)

Now,

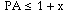
Why? Equality occurs if and only if the vertex A coincides with the endpoint of the diameter determined by OP.

Sooooo. . .

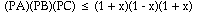
Have you seen this before? See Maximum of f(x) = (1-x)(1+x)(1+x)