

Consider the four vertices of a square. To have a square inscribed in a triangle, two of the square's vertices must lie on the same side of the triangle. Here are some examples:
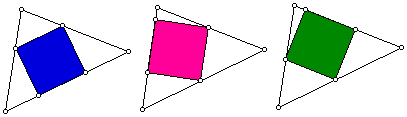
Given a triangle, can we construct the inscribed square?
For the triangle shown above, there are three distinct inscribed squares. What conjectures can you make about number of inscribed squares for a given triangle? Is there any relation between the area of the inscribed square and the given triangle?
Presented by Alan Russell (Guest lecturer) from George Polya's How to Solve It.