

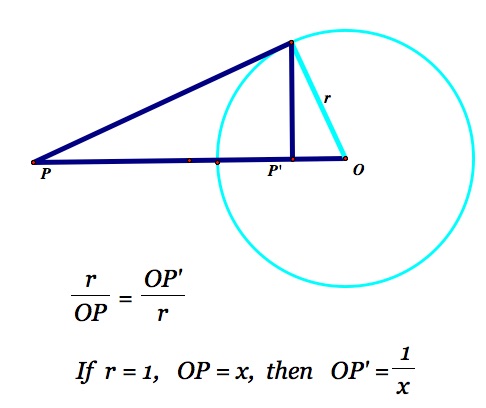
We can develop a mapping of the plane where all points external to a circle
-- Where all points outside a given circle are mapped to points inside the circle
-- Where all points inside the given circle are mapped to points outside the circle
-- Where points on the circle are mapped onto themselves
There is usually no loss of generality to take the circle of inversion to have a radius of r = 1 and so the inverse relationship is given.
Click here for a GSP script tool to implement the mapping.
1. Use the inversion ideas to construct a trisection of a line segment.
2. Develop an inversion procedure for dividing a segment into n equal segments.
3. Show that the inversion a circle that does not go through the center of the inversion circle is another circle. Describe the different possibilities.
4. Show that the inversion of a circle passing through the center of the circle of inversion will have an image that is a line. Describe.
5. Find the images of other curves or figures.
To be continued.