

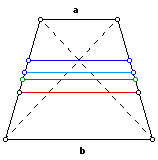
For all of the following problems, take as given (or constructed) a trapezoid with parallel sides of length a and b.
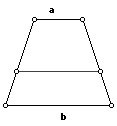
What is the length, in terms of a and b, of a parallel line segment through the midpoints of the slant sides of the trapezoid?
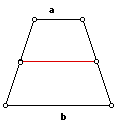
What is the length, in terms of a and b, of a parallel line segment through the intersection of the diagonals of the trapezoid?
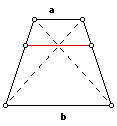
What is the length, in terms of a and b, of a parallel line segment that divides the trapezoid into two similar trapezoids?
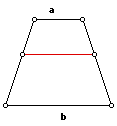
What is the length, in terms of a and b, of a parallel line segment that divides the trapezoid into two trapezoids of equal area?
Compare the four line segements on the same trapezoid. Are they always in the same relative position?
Compare the four formulas.
What inequalities will always hold?
If it is useful to you, a GSP sketch is available by clicking HERE.
Use ruler and compass contructions, or use Geometer's sketchpad,
to construct the line segment parallel to the bases of
length a and b to divide the trapezoid
into two similar trapezoids.
Use ruler and compass contructions, or use Geometer's sketchpad,
to construct the line segment parallel to the bases of
length a and b to divide the trapezoid
into two trapezoids having the same area.
Consider your definition of an trapezoid.
Is a rectangle an isosceles trapezoid?
In this problem, what is the condition in the inequalities when a = b ?
Does your definition of an isosceles trapezoid allow you to demonstrate that point?