Your problem may be modest; but if it challenges your curiosity and brings into play your inventive faculties, and if you solve it by your own means, you may experience the tension and enjoy the triumph of discovery. Such experiences at a susceptible age may create a taste for mental work and leave their imprint on mind and character for a lifetime. (26, p. v.)
Problem solving has a special importance in the study of mathematics. A primary goal of mathematics teaching and learning is to develop the ability to solve a wide variety of complex mathematics problems. Stanic and Kilpatrick (43) traced the role of problem solving in school mathematics and illustrated a rich history of the topic. To many mathematically literate people, mathematics is synonymous with solving problems -- doing word problems, creating patterns, interpreting figures, developing geometric constructions, proving theorems, etc. On the other hand, persons not enthralled with mathematics may describe any mathematics activity as problem solving.
Learning to solve problems is the principal reason for studying mathematics.
National Council of Supervisors of Mathematics (22)
When two people talk about mathematics problem solving, they may not be talking about the same thing. The rhetoric of problem solving has been so pervasive in the mathematics education of the 1980s and 1990s that creative speakers and writers can put a twist on whatever topic or activity they have in mind to call it problem solving! Every exercise of problem solving research has gone through some agony of defining mathematics problem solving. Yet, words sometimes fail. Most people resort to a few examples and a few nonexamples. Reitman (29) defined a problem as when you have been given the description of something but do not yet have anything that satisfies that description. Reitman's discussion described a problem solver as a person perceiving and accepting a goal without an immediate means of reaching the goal. Henderson and Pingry (11) wrote that to be problem solving there must be a goal, a blocking of that goal for the individual, and acceptance of that goal by the individual. What is a problem for one student may not be a problem for another -- either because there is no blocking or no acceptance of the goal. Schoenfeld (33) also pointed out that defining what is a problem is always relative to the individual.
How long is the groove on one side of a long-play (33 1/3 rpm) phonograph record? Assume there is a single recording and the Outer (beginning) groove is 5.75 inches from the center and the Inner (ending) groove is 1.75 inches from the center. The recording plays for 23 minutes.
Mathematics teachers talk about, write about, and act upon,
many different ideas under the heading of problem solving. Some
have in mind primarily the selection and presentation of "good"
problems to students. Some think of mathematics program goals
in which the curriculum is structured around problem content.
Others think of program goals in which the strategies and techniques
of problem solving are emphasized. Some discuss mathematics problem
solving in the context of a method of teaching, i.e., a problem
approach. Indeed, discussions of mathematics problem solving often
combine and blend several of these ideas.
In this chapter, we want to review and discuss the research on
how students in secondary schools can develop the ability to solve
a wide variety of complex problems. We will also address how instruction
can best develop this ability. A fundamental goal of all instruction
is to develop skills, knowledge, and abilities that transfer to
tasks not explicitly covered in the curriculum. Should instruction
emphasize the particular problem solving techniques or strategies
unique to each task? Will problem solving be enhanced by providing
instruction that demonstrates or develops problem solving techniques
or strategies useful in many tasks? We are particularly interested
in tasks that require mathematical thinking (34) or higher order
thinking skills (17). Throughout the chapter, we have chosen to
separate and delineate aspects of mathematics problem solving
when in fact the separations are pretty fuzzy for any of us.
Although this chapter deals with problem solving research at the
secondary level, there is a growing body of research focused on
young children's solutions to word problems (6,30). Readers should
also consult the problem solving chapters in the Elementary and
Middle School volumes.
Educational research is conducted within a variety of constraints -- isolation of variables, availability of subjects, limitations of research procedures, availability of resources, and balancing of priorities. Various research methodologies are used in mathematics education research including a clinical approach that is frequently used to study problem solving. Typically, mathematical tasks or problem situations are devised, and students are studied as they perform the tasks. Often they are asked to talk aloud while working or they are interviewed and asked to reflect on their experience and especially their thinking processes. Waters (48) discusses the advantages and disadvantages of four different methods of measuring strategy use involving a clinical approach. Schoenfeld (32) describes how a clinical approach may be used with pairs of students in an interview. He indicates that "dialog between students often serves to make managerial decisions overt, whereas such decisions are rarely overt in single student protocols."
A nine-digit number is formed using each of the digits 1,2,3,...,9 exactly once. For n = 1,2,3,...,9, n divides the first n digits of the number. Find the number.
The basis for most mathematics problem solving research for
secondary school students in the past 31 years can be found in
the writings of Polya (26,27,28), the field of cognitive psychology,
and specifically in cognitive science. Cognitive psychologists
and cognitive scientists seek to develop or validate theories
of human learning (9) whereas mathematics educators seek to understand
how their students interact with mathematics (33,40). The area
of cognitive science has particularly relied on computer simulations
of problem solving (25,50). If a computer program generates a
sequence of behaviors similar to the sequence for human subjects,
then that program is a model or theory of the behavior. Newell
and Simon (25), Larkin (18), and Bobrow (2) have provided simulations
of mathematical problem solving. These simulations may be used
to better understand mathematics problem solving.
Constructivist theories have received considerable acceptance
in mathematics education in recent years. In the constructivist
perspective, the learner must be actively involved in the construction
of one's own knowledge rather than passively receiving knowledge.
The teacher's responsibility is to arrange situations and contexts
within which the learner constructs appropriate knowledge (45,48).
Even though the constructivist view of mathematics learning is
appealing and the theory has formed the basis for many studies
at the elementary level, research at the secondary level is lacking.
Our review has not uncovered problem solving research at the secondary
level that has its basis in a constructivist perspective. However,
constructivism is consistent with current cognitive theories of
problem solving and mathematical views of problem solving involving
exploration, pattern finding, and mathematical thinking (36,15,20);
thus we urge that teachers and teacher educators become familiar
with constructivist views and evaluate these views for restructuring
their approaches to teaching, learning, and research dealing with
problem solving.
It is useful to develop a framework to think about the processes
involved in mathematics problem solving. Most formulations of
a problem solving framework in U. S. textbooks attribute some
relationship to Polya's (26) problem solving stages. However,
it is important to note that Polya's "stages" were more
flexible than the "steps" often delineated in textbooks.
These stages were described as understanding the problem, making
a plan, carrying out the plan, and looking back.
To Polya (28), problem solving was a major theme of doing mathematics
and "teaching students to think" was of primary importance.
"How to think" is a theme that underlies much of genuine
inquiry and problem solving in mathematics. However, care must
be taken so that efforts to teach students "how to think"
in mathematics problem solving do not get transformed into teaching
"what to think" or "what to do." This is,
in particular, a byproduct of an emphasis on procedural knowledge
about problem solving as seen in the linear frameworks of U. S.
mathematics textbooks (Figure 1) and the very limited problems/exercises
included in lessons. Figure 1: Linear models of problem solving
found in textbooks that are inconsistent with genuine problem
solving.
Clearly, the linear nature of the models used in numerous textbooks does not promote the spirit of Polya's stages and his goal of teaching students to think. By their nature, all of these traditional models have the following defects:
1. They depict problem solving as a linear process.
2. They present problem solving as a series of steps.
3. They imply that solving mathematics problems is a procedure to be memorized, practiced, and habituated.
4. They lead to an emphasis on answer getting.
These linear formulations are not very consistent with genuine
problem solving activity. They may, however, be consistent with
how experienced problem solvers present their solutions and answers
after the problem solving is completed. In an analogous way, mathematicians
present their proofs in very concise terms, but the most elegant
of proofs may fail to convey the dynamic inquiry that went on
in constructing the proof.
Another aspect of problem solving that is seldom included in textbooks
is problem posing, or problem formulation. Although there has
been little research in this area, this activity has been gaining
considerable attention in U. S. mathematics education in recent
years. Brown and Walter (3) have provided the major work on problem
posing. Indeed, the examples and strategies they illustrate show
a powerful and dynamic side to problem posing activities. Polya
(26) did not talk specifically about problem posing, but much
of the spirit and format of problem posing is included in his
illustrations of looking back.
A framework is needed that emphasizes the dynamic and cyclic nature
of genuine problem solving. A student may begin with a problem
and engage in thought and activity to understand it. The student
attempts to make a plan and in the process may discover a need
to understand the problem better. Or when a plan has been formed,
the student may attempt to carry it out and be unable to do so.
The next activity may be attempting to make a new plan, or going
back to develop a new understanding of the problem, or posing
a new (possibly related) problem to work on.
The framework in Figure 2 is useful for illustrating the dynamic,
cyclic interpretation
of Polya's (26) stages. It has been used in a mathematics problem
solving course at the University of Georgia for many years. Any
of the arrows could describe student activity (thought) in the
process of solving mathematics problems. Clearly, genuine problem
solving experiences in mathematics can not be captured by the
outer, one-directional arrows alone. It is not a theoretical model.
Rather, it is a framework for discussing various pedagogical,
curricular, instructional, and learning issues involved with the
goals of mathematical problem solving in our schools.
Problem solving abilities, beliefs, attitudes, and performance
develop in contexts (36) and those contexts must be studied as
well as specific problem solving activities. We have chosen to
organize the remainder of this chapter around the topics of problem
solving as a process, problem solving as an instructional goal,
problem solving as an instructional method, beliefs about problem
solving, evaluation of problem solving, and technology and problem
solving.
Garofola and Lester (10) have suggested that students are largely unaware of the processes involved in problem solving and that addressing this issue within problem solving instruction may be important. We will discuss various areas of research pertaining to the process of problem solving.
To become a good problem solver in mathematics, one must develop
a base of mathematics knowledge. How effective one is in organizing
that knowledge also contributes to successful problem solving.
Kantowski (13) found that those students with a good knowledge
base were most able to use the heuristics in geometry instruction.
Schoenfeld and Herrmann (38) found that novices attended to surface
features of problems whereas experts categorized problems on the
basis of the fundamental principles involved.
Silver (39) found that successful problem solvers were more likely
to categorize math problems on the basis of their underlying similarities
in mathematical structure. Wilson (50) found that general heuristics
had utility only when preceded by task specific heuristics. The
task specific heuristics were often specific to the problem domain,
such as the tactic most students develop in working with trigonometric
identities to "convert all expressions to functions of sine
and cosine and do algebraic simplification."
An algorithm is a procedure, applicable to a particular type of exercise, which, if followed correctly, is guaranteed to give you the answer to the exercise. Algorithms are important in mathematics and our instruction must develop them but the process of carrying out an algorithm, even a complicated one, is not problem solving. The process of creating an algorithm, however, and generalizing it
The creation of an algorithm may involve developing a process for factoring quadratic equations, as well as developing a process for partitioning a line segment using only Euclidian constructions.
to a specific set of applications can be problem solving. Thus problem solving can be incorporated into the curriculum by having students create their own algorithms. Research involving this approach is currently more prevalent at the elementary level within the context of constructivist theories.
Heuristics are kinds of information, available to students in making decisions during problem solving, that are aids to the generation of a solution, plausible in nature rather than prescriptive, seldom providing infallible guidance, and variable in results. Somewhat synonymous terms are strategies, techniques, and rules-of-thumb. For example, admonitions to "simplify an algebraic expression by removing parentheses," to "make a table," to "restate the problem in your own words," or to "draw a figure to suggest the line of argument for a proof" are heuristic in nature. Out of context, they have no particular value, but incorporated into situations of doing mathematics they can be quite powerful (26,27,28).
Many a guess has turned out to be wrong but nevertheless useful in leading to a better one. Polya (26, p. 99)
Theories of mathematics problem solving (25,33,50) have placed
a major focus on the role of heuristics. Surely it seems that
providing explicit instruction on the development and use of heuristics
should enhance problem solving performance; yet it is not that
simple. Schoenfeld (35) and Lesh (19) have pointed out the limitations
of such a simplistic analysis. Theories must be enlarged to incorporate
classroom contexts, past knowledge and experience, and beliefs.
What Polya (26) describes in How to Solve It is far more
complex than any theories we have developed so far.
Mathematics instruction stressing heuristic processes has been
the focus of several studies. Kantowski (14) used heuristic instruction
to enhance the geometry problem solving performance of secondary
school students. Wilson (50) and Smith (42) examined contrasts
of general and task specific heuristics. These studies revealed
that task specific hueristic instruction was more effective than
general hueristic instruction. Jensen (12) used the heuristic
of subgoal generation to enable students to form problem solving
plans. He used thinking aloud, peer interaction, playing the role
of teacher, and direct instruction to develop students' abilities
to generate subgoals.
An extensive knowledge base of domain specific information,
algorithms, and a repertoire of heuristics are not sufficient
during problem solving. The student must also construct some decision
mechanism to select from among the available heuristics, or to
develop new ones, as problem situations are encountered. A major
theme of Polya's writing was to do mathematics, to reflect on
problems solved or attempted, and to think (27,28). Certainly
Polya expected students to engage in thinking about the various
tactics, patterns, techniques, and strategies available to them.
To build a theory of problem solving that approaches Polya's model,
a manager function must be incorporated into the system. Long
ago, Dewey (8), in How we think, emphasized self-reflection in
the solving of problems.
Recent research has been much more explicit in attending to this
aspect of problem solving and the learning of mathematics. The
field of metacognition concerns thinking about one's own cognition.
Metacognition theory holds that such thought can monitor, direct,
and control one's cognitive processes (4,41). Schoenfeld (34)
described and demonstrated an executive or monitor component to
his problem solving theory. His problem solving courses included
explicit attention to a set of guidelines for reflecting about
the problem solving activities in which the students were engaged.
Clearly, effective problem solving instruction must provide the
students with an opportunity to reflect during problem solving
activities in a systematic and constructive way.
Looking back may be the most important part of problem solving.
It is the set of activities that provides the primary opportunity
for students to learn from the problem. The phase was identified
by Polya (26) with admonitions to examine the solution by such
activities as checking the result, checking the argument, deriving
the result differently, using the result, or the method, for some
other problem, reinterpreting the problem, interpreting the result,
or stating a new problem to solve.
Teachers and researchers report, however, that developing the
disposition to look back is very hard to accomplish with students.
Kantowski (14) found little evidence among students of looking
back even though the instruction had stressed it. Wilson (51)
conducted a year long inservice mathematics problem solving course
for secondary teachers in which each participant developed materials
to implement some aspect of problem solving in their on-going
teaching assignment. During the debriefing session at the final
meeting, a teacher put it succinctly: "In schools, there
is no looking back." The discussion underscored the agreement
of all the participants that getting students to engage in looking
back activities was difficult. Some of the reasons cited were
entrenched beliefs that problem solving in mathematics is answer
getting; pressure to cover a prescribed course syllabus; testing
(or the absence of tests that measure processes); and student
frustration.
The importance of looking back, however, outweighs these difficulties.
Five activities essential to promote learning from problem solving
are developing and exploring problem contexts, extending problems,
extending solutions, extending processes, and developing self-reflection.
Teachers can easily incorporate the use of writing in mathematics
into the looking back phase of problem solving. It is what you
learn after you have solved the problem that really counts.
Problem posing (3) and problem formulation (16) are logically
and philosophically appealing notions to mathematics educators
and teachers. Brown and Walter provide suggestions for implementing
these ideas. In particular, they discuss the "What-If-Not"
problem posing strategy that encourages the generation of new
problems by changing the conditions of a current problem. For
example, given a mathematics theorem or rule, students may be
asked to list its attributes. After a discussion of the attributes,
the teacher may ask "what if some or all of the given attributes
are not true?" Through this discussion, the students generate
new problems.
Brown and Walter provide a wide variety of situations implementing
this strategy including a discussion of the development of non-Euclidean
geometry. After many years of attempting to prove the parallel
postulate as a theorem, mathematicians began to ask "What
if it were not the case that through a given external point there
was exactly one line parallel to the given line? What if there
were two? None? What would that do to the structure of geometry?"
(p.47). Although these ideas seem promising, there is little explicit
research reported on problem posing.
If our answer to this question uses words like exploration,
inquiry, discovery, plausible reasoning, or problem solving, then
we are attending to the processes of mathematics. Most of us would
also make a content list like algebra, geometry, number, probability,
statistics, or calculus. Deep down, our answers to questions such
as What is mathematics? What do mathematicians do? What do mathematics
students do? Should the activities for mathematics students model
what mathematicians do? can affect how we approach mathematics
problems and how we teach mathematics.
The National Council of Teachers of Mathematics (NCTM) (23,24)
recommendations to make problem solving the focus of school mathematics
posed fundamental questions about the nature of school mathematics.
The art of problem solving is the heart of mathematics. Thus,
mathematics instruction should be designed so that students experience
mathematics as problem solving.
The National Council of Teachers of Mathematics recommends that --
l. problem solving be the focus of school mathematics in the 1980s.
An Agenda for Action (23)
We strongly endorse the first recommendation of An Agenda for Action. The initial standard of each of the three levels addresses this goal.
Curriculum and Evaluation Standards (24)
The NCTM (23,24) has strongly endorsed the inclusion of problem
solving in school mathematics. There are many reasons for doing
this.
First, problem solving is a major part of mathematics. It is the
sum and substance of our discipline and to reduce the discipline
to a set of exercises and skills devoid of problem solving is
misrepresenting mathematics as a discipline and shortchanging
the students. Second, mathematics has many applications and often
those applications represent important problems in mathematics.
Our subject is used in the work, understanding, and communication
within other disciplines. Third, there is an intrinsic motivation
embedded in solving mathematics problems. We include problem solving
in school mathematics because it can stimulate the interest and
enthusiasm of the students. Fourth, problem solving can be fun.
Many of us do mathematics problems for recreation. Finally, problem
solving must be in the school mathematics curriculum to allow
students to develop the art of problem solving. This art is so
essential to understanding mathematics and appreciating mathematics
that it must be an instructional goal.
Teachers often provide strong rationale for not including problem
solving activities is school mathematics instruction. These include
arguments that problem solving is too difficult, problem solving
takes too much time, the school curriculum is very full and there
is no room for problem solving, problem solving will not be measured
and tested, mathematics is sequential and students must master
facts, procedures, and algorithms, appropriate mathematics problems
are not available, problem solving is not in the textbooks, and
basic facts must be mastered through drill and practice before
attempting the use of problem solving. We should note, however,
that the student benefits from incorporating problem solving into
the mathematics curriculum as discussed above outweigh this line
of reasoning. Also we should caution against claiming an emphasize
on problem solving when in fact the emphasis is on routine exercises.
From various studies involving problem solving instruction, Suydam
(44) concluded:
If problem solving is treated as "apply the procedure," then the students try to follow the rules in subsequent problems. If you teach problem solving as an approach, where you must think and can apply anything that works, then students are likely to be less rigid. (p. 104)
Problem solving as a method of teaching may be used to accomplish the instructional goals of learning basic facts, concepts, and procedures, as well as goals for problem solving within problem contexts. For example, if students investigate the areas of all triangles having a fixed perimeter of 60 units, the problem solving activities should provide ample practice in computational skills and use of formulas and procedures, as well as opportunities for the conceptual development of the relationships between area and perimeter. The "problem" might be to find the triangle with the most area, the areas of triangles with integer sides, or a triangle with area numerically equal to the perimeter. Thus problem solving as a method of teaching can be used to introduce concepts through lessons involving exploration and discovery. The creation of an algorithm, and its refinement, is also a complex problem solving task which can be accomplished through the problem approach to teaching. Open ended problem solving often uses problem contexts, where a sequence of related problems might be explored. For example, the problems in the margins evolved from considering gardens of different shapes that could be enclosed with 100 yards of fencing.
Suppose one had 100 yards of fencing to enclose a garden. What shapes could be enclosed? What are the dimensions of each and what is the area? Make a chart.
What triangular region with P = 100 has the most area?
Find all five triangular regions with P = 100 having integer sides and integer area. (such as 29, 29, 42)
What rectangular regions could be enclosed? Areas? Organize a table? Make a graph?
Which rectangular region has the most area? from a table? from a graph? from algebra, using the arithmetic mean-geometric mean inequality?
What is the area of a regular hexagon with P = 100?
What is the area of a regular octagon with P = 100?
What is the area of a regular n-gon with P = 100? Make a table for n = 3 to 25. Make a graph. What happens to 1/n(tan 180/n) as n increases?
What if part of the fencing is used to build a partition perpendicular to a side? Consider a rectangular region with one partition? With 2 partitions? with n partitions? (There is a surprise in this one!!) What if the partition is a diagonal of the rectangle?
What is the maximum area of a sector of a circle with P = 100? (Here is another surprise!!! -- could you believe it is r2 when r = 25? How is this similar to a square being the maximum rectangle and the central angle of the maximum sector being 2 radians?)
What about regions built along a natural boundary? For example the maximum for both a rectangular region and a triangular region built along a natural boundary with 100 yards of fencing is 1250 sq. yds. But the rectangle is not the maximum area four-sided figure that can be built. What is the maximum-area four-sided figure?
Many teachers in our workshops have reported success with a
"problem of the week" strategy. This is often associated
with a bulletin board in which a challenge problem is presented
on a regular basis (e.g., every Monday). The idea is to capitalize
on intrinsic motivation and accomplishment, to use competition
in a constructive way, and to extend the curriculum. Some teachers
have used schemes for granting "extra credit" to successful
students. The monthly calendar found in each issue of The Mathematics
Teacher is an excellent source of problems.
Whether the students encounter good mathematics problems depends
on the skill of the teacher to incorporate problems from various
sources (often not in textbooks). We encourage teachers to begin
building a resource book of problems oriented specifically to
a course in their on-going workload. Good problems can be found
in the Applications in Mathematics (AIM Project) materials
(21) consisting of video tapes, resource books and computer diskettes
published by the Mathematical Association of America. These problems
can often be extended or modified by teachers and students to
emphasize their interests. Problems of interest for teachers and
their students can also be developed through the use of The
Challenge of the Unknown materials (1) developed by the American
Association for the Advancement of Science. These materials consist
of tapes providing real situations from which mathematical problems
arise and a handbook of ideas and activities that can be used
to generate other problems.
The importance of students' (and teachers') beliefs about mathematics problem solving lies in the assumption of some connection between beliefs and behavior. Thus, it is argued, the beliefs of mathematics students, mathematics teachers, parents, policy makers, and the general public about the roles of problem solving in mathematics become prerequisite or co-requisite to developing problem solving. The Curriculum and Evaluation Standards makes the point that "students need to view themselves as capable of using their growing mathematical knowledge to make sense of new problem situations in the world around them" (24, p. ix.). We prefer to think of developing a sense of "can do" in our students as they encounter mathematics problems.
The first rule of teaching is to know what you are supposed to teach. The second rule of teaching is to know a little more than what you are supposed to teach. . . . Yet it should not be forgotten that a teacher of mathematics should know some mathematics, and that a teacher wishing to impart the right attitude of mind toward problems to his students should have acquired that attitude himself. Polya (26, p. 173).
Schoenfeld (36,37) reported results from a year-long study
of detailed observations, analysis of videotaped instruction,
and follow-up questionnaire data from two tenth-grade geometry
classes. These classes were in select high schools and the classes
were highly successful as determined by student performance on
the New York State Regent's examination. Students reported beliefs
that mathematics helps them to think clearly and they can be creative
in mathematics, yet, they also claimed that mathematics is learned
best by memorization. Similar contrasts have been reported for
the National Assessment (5). Indeed our conversations with teachers
and our observations portray an overwhelming predisposition of
secondary school mathematics students to view problem solving
as answer getting, view mathematics as a set of rules, and be
highly oriented to doing well on tests.
Schoenfeld (37) was able to tell us much more about the classes
in his study. He makes the following points.
The rhetoric of problem solving has become familiar over the past decade. That rhetoric was frequently heard in the classes we observed -- but the reality of those classrooms is that real problems were few and far between . . . virtually all problems the students were asked to solve were bite-size exercises designed to achieve subject matter mastery: the exceptions were clearly peripheral tasks that the students found enjoyable but that they considered to be recreations or rewards rather than the substance they were expected to learn . . . the advances in mathematics education in the [past] decade . . . have been largely in our acquiring a more enlightened goal structure, and having students pick up the rhetoric -- but not the substance -- related to those goals. (pp. 359-9)
Each of us needs to ask if the situation Schoenfeld describes is similar to our own school. We must take care that espoused beliefs about problem solving are consistent with a legitimately implemented problem solving focus in school mathematics.
The appropriate use of technology for many people has significant identity with mathematics problem solving. This view emphasizes the importance of technology as a tool for mathematics problem solving. This is in contrast to uses of technology to deliver instruction or for generating student feedback.
In the past, problem solving research involving technology has often dealt with programming as a major focus. This research has often provided inconclusive results. Indeed, the development of a computer program to perform a mathematical task can be a challenging mathematical problem and can enhance the programmer's understanding of the mathematics being used. Too often, however, the focus is on programming skills rather than on using programming to solve mathematics problems. There is a place for programming within mathematics study, but the focus ought to be on the mathematics problems and the use of the computer as a tool for mathematics problem solving.
Iteration and recursion are concepts of mathematics made available
to the secondary school level by technology. Students may implement
iteration by writing a computer program, developing a procedure
for using a calculator, writing a sequence of decision steps,
or developing a classroom dramatization. The approximation of
roots of equations can be made operational with a calculator or
computer to carry out the iteration.
For example, the process for finding the three roots of
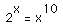
is not very approachable without iterative techniques. Iteration
is also useful when determining the maximum height, h, between
a chord and an arc of a circle when the length S of the arc and
the length L of the chord are known. This may call for solving
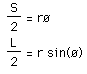
simultaneously and using iterative techniques to find the radius r and and central angle ø in order to evaluate h = r - r cos ø. Fractals can also be explored through the use of iterative techniques and computer software.
Technology can be used to enhance or make possible exploration
of conceptual or problem situations. For example, a function grapher
computer program or a graphics calculator can allow student exploration
of families of curves such as
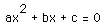
for different values of a, b, and c.
A calculator can be used to explore sequences such as
for different values of a. In this way, technology introduces
a dynamic aspect to investigating mathematics.
Thomas (46) studied the use of computer graphic problem solving
activities to assist in the instruction of functions and transformational
geometry at the secondary school level. The students were challenged
to create a computer graphics design of a preselected picture
using graphs of functions and transformational geometry. Thomas
found these activities helped students to better understand function
concepts and improved student attitudes.
As the emphasis on problem solving in mathematics classrooms increases, the need for evaluation of progress and instruction in problem solving becomes more pressing. It no longer suffices for us to know which kinds of problems are correctly and incorrectly solved by students. As Schoenfeld (36) describes:
All too often we focus on a narrow collection of well-defined tasks and train students to execute those tasks in a routine, if not algorithmic fashion. Then we test the students on tasks that are very close to the ones they have been taught. If they succeed on those problems, we and they congratulate each other on the fact that they have learned some powerful mathematical techniques. In fact, they may be able to use such techniques mechanically while lacking some rudimentary thinking skills. To allow them, and ourselves, to believe that they "understand" the mathematics is deceptive and fraudulent. (p. 30)
Schoenfeld (31) indicates that capable mathematics students
when removed from the context of coursework have difficulty doing
what may be considered elementary mathematics for their level
of achievement. For example, he describes a situation in which
he gave a straightforward theorem from tenth grade plane geometry
to a group of junior and senior mathematics majors at the University
of California involved in a problem solving course. Of the eight
students solving this problem only two made any significant progress.
We need to focus on the teaching and learning of mathematics and,
in turn, problem solving using a holistic approach. As recommended
in the NCTM's An Agenda for Action (23), "the success
of mathematics programs and student learning [must] be evaluated
by a wider range of measures than conventional testing" (p.
1). Although this recommendation is widely accepted among mathematics
educators, there is a limited amount of research dealing with
the evaluation of problem solving within the classroom environment.
Classroom research: Ask your students to keep a problem solving notebook in which they record on a weekly basis:
(1) their solution to a mathematics problem.
(2) a discussion of the strategies they used to solve the problem.
(3) a discussion of the mathematical similarities of this problem with other problems they have solved.
(4) a discussion of possible extensions for the problem.
(5) an investigation of at least one of the extensions they discussed.Use these notebooks to evaluate students' progress. Then periodically throughout the year, analyze the students' overall progress as well as their reactions to the notebooks in order to asses the effectiveness of the evaluation process.
Some research dealing with the evaluation of problem solving
involves diagnosing students' cognitive processes by evaluating
the amount and type of help needed by an individual during a problem
solving activity. Campione, Brown, and Connell (4) term this method
of evaluation as dynamic assessment. Students are given mathematics
problems to solve. The assessor then begins to provide as little
help as necessary to the students throughout their problem solving
activity. The amount and type of help needed can provide good
insight into the students' problem solving abilities, as well
as their ability to learn and apply new principles. Trismen (47)
reported the use of hints to diagnosis student difficulties in
problem solving in high school algebra and plane geometry. Problems
were developed such that the methods of solutions where not readily
apparent to the students. A sequence of hints was then developed
for each item. According to Trismen, "the power of the hint
technique seems to lie in its ability to identify those particular
students in need of special kinds of help" (p. 371).
Campione and his colleagues (4) also discussed a method to help
monitor and evaluate the progress of a small cooperative group
during a problem solving session. A learning leader (sometimes
the teacher sometimes a student) guides the group in solving the
problem through the use of three boards: (1) a Planning Board,
where important information and ideas about the problem are recorded,
(2) a Representation Board, where diagrams illustrating the problems
are drawn, and (3) a Doing Board, where appropriate equations
are developed and the problem is solved. Through the use of this
method, the students are able to discuss and reflect on their
approaches by visually tracing their joint work. Campione and
his colleagues indicated that increased student engagement and
enthusiasm in problem solving, as well as, increased performance
resulted from the use of this method for solving problems.
Methods, such as the clinical approach discussed earlier, used
to gather data dealing with problem solving and individual's thinking
processes may also be used in the classroom to evaluate progress
in problem solving. Charles, Lester, and O'Daffer (7) describe
how we may incorporate these techniques into a classroom problem
solving evaluation program. For example, thinking aloud may be
canonically achieved within the classroom by placing the students
in cooperative groups. In this way, students may express their
problem solving strategies aloud and thus we may be able to assess
their thinking processes and attitudes unobtrusively. Charles
and his colleagues also discussed the use of interviews and student
self reports during which students are asked to reflect on their
problem solving experience a technique often used in problem solving
research. Other techniques which they describe involve methods
of scoring students' written work. Figure 3 illustrates a final
assignment used to assess teachers' learning in a problem solving
course that has been modified to be used with students at the
secondary level.
1. (20 points)
Select a problem that you have worked on but not yet solved, and that you feel you can eventually solve. Present the following:a. Show or describe what you have done so far (It could be that you tell me where to find your work in your notebook).
b. Assess how you feel about the problem. Is the lack of closure a concern? Why?
c. Assess what you may have learned in working on the problem so far.
2. (20 points)a. Select a mathematics theorem or rule from class and make a list of its attributes?
b. Generate at least three new problems by considering the question:
"What if some or all of the given attributes are not true?"
c. Thoroughly investigate one of the problems generated above.
3. (10 points)
Find the maximum area of a trapezoid inscribed in a semicircle of radius 1.
Hint: Use the arithmetic mean-geometric mean inequality
a. Describe your solution.
b. Discuss possible extensions.
Testing, unfortunately, often drives the mathematics curriculum. Most criterion referenced testing and most norm referenced testing is antithetical to problem solving. Such testing emphasizes answer getting. It leads to pressure to "cover" lots of material and teachers feel pressured to forego problem solving. They may know that problem solving is desirable and developing understanding and using appropriate technology are worthwhile, but ... there is not enough time for all of that and getting ready for the tests. However, teachers dedicated to problem solving have been able to incorporate problem solving into their mathematics curriculum without bringing down students' scores on standardized tests. Although test developers, such as the designers of the California Assessment Program, are beginning to consider alternative test questions, it will take time for these changes to occur. By committing ourselves to problem solving within our classrooms, we will further accentuate the need for changes in testing practices while providing our students with invaluable mathematics experiences.
We are struck by the seemingly contradictory facts that there is a vast literature on problem solving in mathematics and, yet, there is a multitude of questions to be studied, developed, and written about in order to make genuine problem solving activities an integral part of mathematics instruction.
Thus a teacher of mathematics has a great opportunity. If he fills his allotted time with drilling his students in routine operations he kills their interest, hampers their intellectual development, and misuses his opportunity. But if he challenges the curiosity of his students by setting them problems proportionate to their knowledge, and helps them to solve their problems with stimulating questions, he may give them a taste for, and some means of, independent thinking. Polya (26, p. v.)
Further, although many may view this as primarily a curriculum question, and hence call for restructured textbooks and materials, it is the mathematics teacher who must create the context for problem solving to flourish and for students to become problem solvers. The first one in the classroom to become a problem solver must be the teacher.
The primary goal of most students in mathematics classes is to see an algorithm that will give them the answer quickly. Students and parents struggle with (and at times against) the idea that math class can and should involve exploration, conjecturing, and thinking. When students struggle with a problem, parents often accuse them of not paying attention in class; "surely the teacher showed you how to work the problem!" How can parents, students, colleagues, and the public become more informed regarding genuine problem solving? How can I as a mathematics teacher in the secondary school help students and their parents understand what real mathematics learning is all about?
*1. American Association for the Advancement of Science. (1986).
The challenge of the unknown. New York: Norton.
2. Bobrow, D. G. (1964). Natural language input for a computer
problem solving system. Unpublished doctoral dissertation, Massachusetts
Institute of Technology, Boston.
*3. Brown, S. I. & Walter, M. I. (1983). The art of problem
posing. Hillsdale, NJ: Lawrence Erlbaum.
*4. Campione, J. C., Brown, A. L., & Connell, M. L. (1988).
Metacognition: On the importance of understanding what you are
doing. In R. I. Charles & E. A. Silver (Eds.), The teaching
and assessing of mathematical problem solving (pp. 93-114). Reston,
VA: Lawrence Erlbaum, National Council of Teachers of Mathematics.
5. Carpenter, T. P., Lindquist, M. M., Matthews, W., & Silver,
E. A. (1983). Results of the third NAEP mathematics assessment:
Secondary school. Mathematics Teacher, 76 (9), 652-659.
6. Carpenter, T. P., Moser, J. M., & Romberg, T. A. (Eds.)
(1982). Addition and subtraction: A cognitive perspective. Hillsdale,
NJ: Lawrence Erlbaum.
*7. Charles, R. I., Lester, F. K., & O'Daffer, P. (1987).
How to evaluate progress in problem solving. Reston, VA: National
Council of Teachers of Mathematics.
8. Dewey, J. (1933). How we think: A restatement of the relation
of reflective thinking to the educative process. Boston: Heath.
9. Frederiksen, N. (1984). Implications of cognitive theory for
instruction in problem solving. Review of Educational Research,
54, 363-407.
10. Garfola, J. & Lester, F. K. (1985). Metacognition, cognitive
monitoring, and mathematical performance. Journal for Research
in Mathematics Education, 16, 163-176.
11. Henderson, K. B. & Pingry, R. E. (1953). Problem solving
in mathematics. In H. F. Fehr (Ed.), The learning of mathematics:
Its theory and practice (21st Yearbook of the National Council
of Teachers of Mathematics) (pp. 228-270). Washington, DC: National
Council of Teachers of Mathematics.
12. Jensen, R. (1984). A multifaceted instructional approach for
developing subgoal generation skills. Unpublished doctoral dissertation,
The University of Georgia.
13. Kantowski, M. G. (1974). Processes involved in mathematical
problem solving. Unpublished doctoral dissertation, The University
of Georgia, Athens.
14. Kantowski, M. G. (1977). Processes involved in mathematical
problem solving. Journal for Research in Mathematics Education,
8, 163-180.
15. Kaput, J. J. (1979). Mathematics learning: Roots of epistemological
status. In J. Lochhead and J. Clement (Eds.), Cognitive process
instruction. Philadelphia, PA: Franklin Institute Press.
16. Kilpatrick, J. (1987). Problem formulating: Where do good
problems come from? In A. H. Schoenfeld (Ed.), Cognitive science
and mathematics education (pp. 123-147). Hillsdale, NJ: Lawrence
Erlbaum.
17. Kulm, G. (Ed.) (1990). Assessing higher order thinking skills.
Washington, D.C.: American Association for the Advancement of
Science.
18. Larkin, J. (1980). Teaching problem solving in physics: The
psychological laboratory and the practical classroom. In F. Reif
& D. Tuma (Eds.), Problem solving in education: Issues in
teaching and research. Hillsdale, NJ: Lawrence Erlbaum.
19. Lesh, R. (1981). Applied mathematical problem solving. Educational
Studies in Mathematics, 12(2), 235-265.
20. Lochhead, J. (1979). An introduction to cognitive process
instruction. In J. Lochhead and J. Clement (Eds.). Cognitive process
instruction. Philadelphia, PA: Franklin Institute Press.
*21. Mathematical Association of America. (1986). Applications
in mathematics (AIM Project materials). Washington, DC: The Author.
22. National Council of Supervisors of Mathematics. (1978). Position
paper on basic mathematical skills. Mathematics Teacher, 71(2),
147-52. (Reprinted from position paper distributed to members
January 1977.)
23. National Council of Teachers of Mathematics. (1980). An agenda
for action: Recommendations for school mathematics in the 1980s.
Reston, VA: The Author.
24. National Council of Teachers of Mathematics. (1989). Curriculum
and evaluation standards for school mathematics. Reston, VA: The
Author.
25. Newell, A. & Simon, H. A. (1972). Human problem solving.
Englewood Cliffs, NJ: Prentice Hall.
*26. Polya, G. (1973). How to solve it. Princeton, NJ: Princeton
University Press. (Originally copyrighted in 1945).
27. Polya, G. (1962). Mathematical discovery: On understanding,
learning and teaching problem solving (vol. 1). New York: Wiley.
28. Polya, G. (1965). Mathematical discovery: On understanding,
learning and teaching problem solving (vol. 2). New York: Wiley.
29. Reitman, W. R. (1965). Cognition and thought. New York: Wiley.
30. Riley, M.S., Greeno, J. G., & Heller, J. I. (1983). Development
of children's problem-solving ability in arithmetic. In H. Ginsburg
(Ed.), The development of mathematical thinking (pp. 153-200).
New York: Academic Press.
31. Schoenfeld, A. H. (1979). Can heuristics be taught? In J.
Lockhead, Cognitive process instruction. Philadelphia, PA: Franklin
Institute Press.
32. Schoenfeld, A. H. (1983). Episodes and executive decisions
in mathematics problem solving. In R. Lesh & M. Landau, Acquisition
of mathematics concepts and processes. New York: Academic Press
33. Schoenfeld, A. H. (1985). Mathematical problem solving. Orlando,
FL: Academic Press.
34. Schoenfeld, A. H., (1985). Metacognitive and epistemological
issues in mathematical understanding. In E. A. Silver, Teaching
and learning mathematical problem solving: Multiple research perspectives
(pp. 361-379). Hillsdale, NJ: Lawrence Erlbaum.
35. Schoenfeld, A. H. (1987). Cognitive science and mathematics
education: An overview. In A. H. Schoenfeld, Cognitive science
and mathematics education. Hillsdale, NJ: Lawrence Erlbaum.
36. Schoenfeld, A. H. (1988). When good teaching leads to bad
results: The disasters of "well taught" mathematics
classes. Educational Psychologist, 23, 145-166.
37. Schoenfeld, A. H. (1989). Explorations of students' mathematical
beliefs and behavior. Journal for Research in Mathematics Education,
20, 338-355.
38. Schoenfeld, A. H., & Herrmann, D. (1982). Problem perception
and knowledge structure in expert and novice mathematical problem
solvers. Journal of Experimental Psychology: Learning, Memory
and Cognition, 8, 484-494.
39. Silver, E. A. (1979). Student perceptions of relatedness among
mathematical verbal problems. Journal for Research in Mathematics
Education, 10(3), 195-210.
40. Silver, E. A. (1987). Foundations of cognitive theory and
research for mathematics problem-solving instruction. In A. H.
Schoenfeld (Ed.), Cognitive science and mathematics education
(pp. 33-60). Hillsdale, NJ: Lawrence Erlbaum.
41. Silver, E. A., Branca, N., & Adams, V. (1980). Metacognition:
The missing link in problem solving? In R. Karplus, (Ed.), Proceedings
of the fourth international conference for the psychology of mathematics
education. Berkeley, CA: PME.
42. Smith, J. P. (1974). The effects of general versus specific
heuristics in mathematical problem-solving tasks (Columbia University,
1973). Dissertation Abstracts International, 34, 2400A.
43. Stanic, G., & Kilpatrick, J. (1988). Historical Perspectives
on Problem Solving in the Mathematics Curriculum. In R. I. Charles
& E. A. Silver (Eds.), The teaching and assessing of mathematical
problem solving (pp. 1-22). Reston, VA: National Council of Teachers
of Mathematics.
44. Suydam, M. (1987). Indications from research on problem solving.
In F. R. Curcio (Ed.), Teaching and learning: A problem solving
focus. Reston, VA: National Council of Teachers of Mathematics.
45. Steffe, L. P., & Wood, T. (Eds.). (1990). Transforming
Children's Mathematical Education. Hillsdale, NJ: Lawrence Erlbaum.
46. Thomas, E. J. Jr. (1990). A study of the effects of a computer
graphics problem-solving activity on student achievements, attitudes,
and task motivation. (Georgia State University, 1989). Dissertation
Abstracts International, 51, 102A.
47. Trismen, D. A. (1988). Hints: An aid to diagnosis in mathematical
problem solving. Journal for Research in Mathematics Education,
19, 358-361.
48. von Glasersfeld, E. (1989). Constructivism in education. In
T. Husen & T. N. Postlethwaite (Eds.), The international encyclopedia
of education. (pp. 162-163). (Suppl. Vol. I). New York: Pergammon.
49. Waters, W. (1984). Concept acquisition tasks. In G. A. Goldin
& C. E. McClintock (Eds.), Task variables in mathematical
problem solving (pp. 277-296). Philadelphia, PA: Franklin Institute
Press.
50. Wilson, J. W. (1967). Generality of heuristics as an instructional
variable. Unpublished Doctoral Dissertation, Stanford University,
San Jose, CA.
51. Wilson, J. W. (1990) Report of the Georgia Plan problem solving
workshop, 1989-90. Unpublished document, The University of Georgia,
Athens.
Wilson, P. S. (Ed.)(1993). Research Ideas for the Classroom: High School Mathematics. New York: MacMillan.
The book was part of the National Council of Teacher of Mathematics
Research Interpretation Project, directed by Sigrid Wagner.
