Discussion and Solution

For a fixed circle and a point X, construct perpendicular segments AC and BD, with the points A, B, C, and D on the circle. Let O be the center of the circle and Y the foot of a perpendicular from O to AC.

Let x be the measure of angle XOY, where OY is the perpendicular to AC, r is the radius of the circle, p is the length of  OY, and d is the length of OX. Then

Likewise, BD, being perpendicular to AC, is

Now, let the sum of the lengths of the diagonals, AC + BD, be

and the area of the quadrilateral ABCD is one-half the product of the two diagonals, so let that be

Evaluating f'(x) and g'(x) we will find that both are 0 for the same values of x, namely

for any integer k. If k is 0 or even, then

.
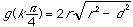
These are the cases where one of the diagonals is a diameter of the circle and the other is a chord perpendicular to it. If k is odd, then

.
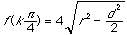
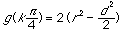
These are the cases where the two diagonals are of equal length. Thus the both the area and the sum of the diagonals reach a minimum when the quadrilateral ABCD is a kite with its longest diagonal a diameter of the circle. Both the area and the sum of the diagonals reach a maximum when quadrilateral ABCD is an isosceles trapezoid with the two diagonals of the same length.

It is also useful to examine graphs of the functions for the area and for the sum of the diagonals. The following graphs show g(x) and f(x) on the same axes with x in the range from 0 to 2.

 

 

 

 

If we construct segments parallel to AC through B and D and segments parallel to BD through A and C in order to define a rectangle with length AC, width BD, and area twice that of quadrilateral ABCD.



For the maximum area and the maximum sum of the diagonals, the total rectangle is a square; for the minimum area and minimum sum of the diagonals, the rectangle is the largest length (2r) and the smallest width .