Triangles and the Medians

Given a triangle ABC and its medians AD, BE, and CF, construct a triangle with sides the same length as the three medians.

a. Show that the triangle is unique. Use GSP to have a linked construction. That is, if triangle ABC is changed, then the corresonding triangle of medians changes also.

b. Show that the area of the triangle of medians is three-fourths of the area of the given triangle.

c. Show that the ratio of the perimeter of the triangle of medians to the perimeter of the given triangle is between .75 and 1.0.

See EMT 668 Assignment 6, Items 1, 2, & 3.

Prove that a median of a triangle divides the triangle into two equal areas.

Hint:

 

Prove that the three medians of a triangle divide the triangle into six equal areas.

Prove that the three medians of a triangle are concurrent.
Given three segments that are the medians of a triangle, show a construction for the triangle.
Prove that the area of a triangle is given by

 

where u, v, and w are lengths of the triangle's medians.

(Problem 4651, Proposed by Khiem V. (Thomas) Ngo, Falls Church, VA., in School Science and Mathematics, Volume 98, Number 2, February 1998, p. 110.)

Useful Result: The triangle formed by the medians of a given triangle will have an area three-fourths the area of the given triangle.

If ABC is a triangle with medians of lengths u, v, and w, and CGF is a triangle with sides the same length as these medians then the ratio of the area of triangle ABC to the area of triangle CGF is 4 to 3. The triangle CGF can be constructed by making segment FG parallel and congruent to median BE and segment CG parallel and congruent to median AD. The ratio of the areas can be proved in several ways, but suffice to see triangle AFC is half the area of ABC, triangle CHF is half the area of triangle CGF, and triangle AHF is one fourth the area of triangle AFC. Therefore the ratio of the areas of triangle AFC to FHC is 4 to 3 and so the ratio of the area of triangle ABC to CGF is 4 to 3.

 

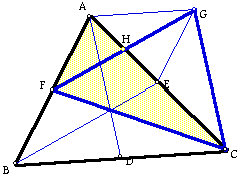
Next step.

Use Heron's formula for the area of the triangle with sides of length u, v, and w. The area of the triangle with medians of length u, v, and w is

 

where .

Substituting and simplifying leads to the result.

The Details (if you need them).

Return to the EMAT 4600/6600 Page