Theorem of Menelaus
Note:
For plane geometry, the Theorem of Menelaus is -- given any line that transverses (crosses) the three sides of a triangle (one of them will have to be extended), six segments are cut off on the sides. The product of three non-adjacent segments is equal to the product of the other three. The converse also holds.
In the figure one set of three non-adjacent segments is AH, BG, and FC; the other set is BH, GC, and AC.
Usually, the two products are expressed in a ratio equal to 1 or equal to -1 if directed segments are used.
The Theorem of Menelaus is perhaps a misnomer. Menelaus produced an analogous theorem for spherical geometry. The theorem for the geometry of the plane was known before Menelaus. Most geometry references, however, cite this theorem for plane geometry as Menelaus's Theorem.
Take any triangle ABC.
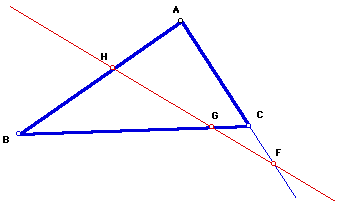Construct a line that transverses all three sides. Note that
one of the sides will have to be extended to get the intersection
point. Let the intersection of the transversal with AC be F, with
BC be G, and with AB be H.
Click here for a GSP demonstration of the proof of Menelaus's Theorem.
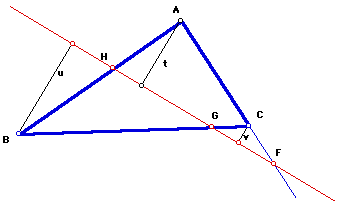
Hint: Construct perpendiculars from the vertices A, B, and C to the transversal. Let their lengths be v, t, and u as shown.
Prove:
The Converse: If three points taken on the three sides of a triangle determine six segments such that the ratio of the products of non-adjacent sides is 1, then the three points are collinear.
Hint: Use indirect proof.
Exploration:
A transversal cuts the sides of the triangle either exactly two internally and one externally, or all three externally. Does Menelaus's theorem hold when the transversal cuts all three sides externally?