

Problem Set 4.2
Problem 4.2.2 See GSP file
Note: If ABCD with AB = BC is not convex, there are other cases:
a. A, B, C, and D are in the same plane and ABCD is concave
b. A, B, C, and D are not in the same plane.
c. ABCD not a simple polygon. That is, for example, D may be located so that BC and DA will cross.
Click HERE to see one solution
Click HERE to see a solution by Brian Swanagan
GSP File for Problems 4.2.6 Solutions
Problem 4.2.7 See GSP File
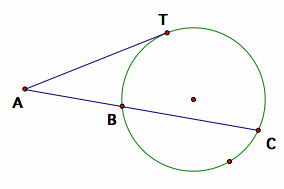
Problem 4.2.8
M, B, and T are on a circle with center O. A tangent is drawn through T that intersects the line MB at A. Do the following:
a. If AM = MB = a, find AT in terms of a.
b. If A is a point in the exterior of the circle, construct a secant through A that intersects the line MB at A such that M is the midpoint of AB. Investigate the construction, describe the steps in the construction, and prove the construction is valid.
Can this Problem and its solution be adapted to provide an alternative way for constructing the Geometry Mean?
Problem 4.2.14 (Note error in the textbook problem statement)
Problem 4.2.15
Problem 4.2.17
Click HERE to see alternative solutions to Part (a) and the construction for Part (b).