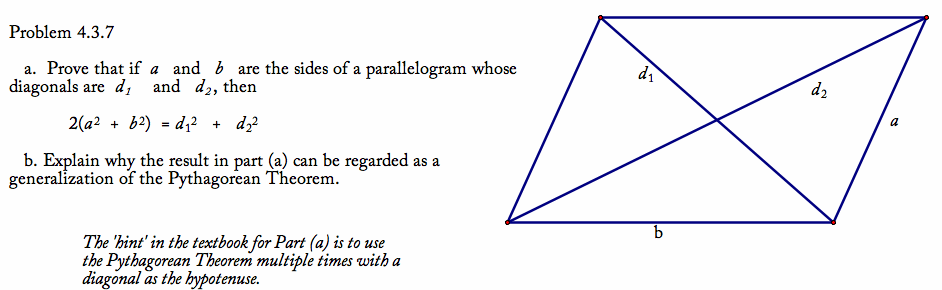Problem Set 4.3
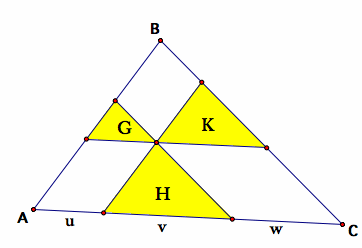1. In the interior of triangle ABC, lines parallel to the sides of the triangle are drawn through a point P. They divide the triangle into six parts, three of which are triangles. If those three triangles have areas of G, H, and K, respectively, find the area of triangle ABC.
From Example 4.4, we see an analogous problem with two subtriangles. Thus we could use the results from Example 4.4 to adapt to this problem or we could use the method of Example 4.4 and carry it out for this problem.
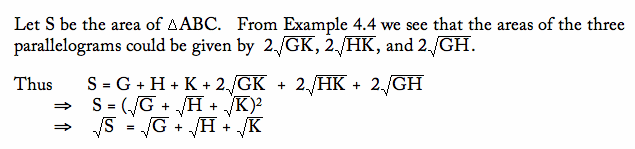
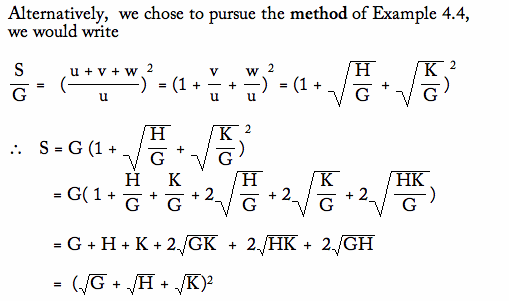
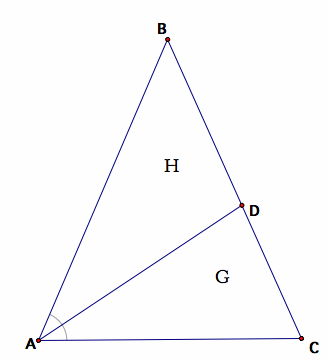
Problem 4.3.3.
Given a parallelogram, construct two parallel lines to one of the diagonals and divide the parallelogram into three parts of equal area.
Plan: If we use the diagonal of the parallelogram two triangles of the same area are created. If each of these two triangles is divided by a line parallel to that diagonal of the parallelogram such that one-third of the area is between the line and the diagonal, then the two lines constructed in this way will be the desired lines to divide the parallelogram into three equal areas.
GSP file with Solution by Jackie Ruff
Problem 4.3.4.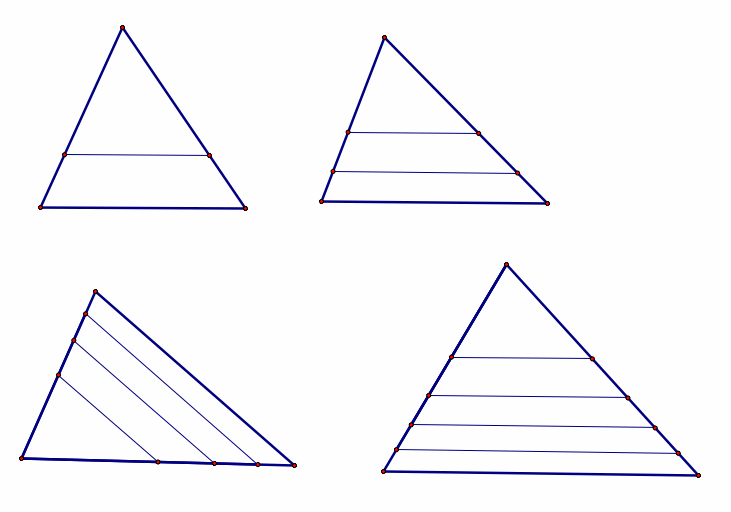 
Given an arbitrary triangle, divide it into n parts of n equal area using lines parallel to the sides. Solve the problem for n = 2, 3, 4, and 5.
Problem 4.3.5.
In a regular hexagon of side a, a second hexagon is inscribed by joining the midpoints of the sides of the first hexagon. In a like manner a third hexagon is inscribed in the second, and so on indefinitely.
a. What is the ratio of the area of the first hexagon to the area of the sixth hexagon?
b. Prove that the areas of the hexagons constitute a geometric sequence.
Problem 4.3.5 GSP file for Solution from Laura Lowe
Problem 4.3.6A (From textbook)
Construct a line parallel to a given line (line n) that will divide triangle ABC into two parts of equal area. Investigate the construction, describe your construction, and prove that it is valid.
See GSP file for Solution by Brian Swanagan and Nick Gomez
Problem 4.3.6B (From me)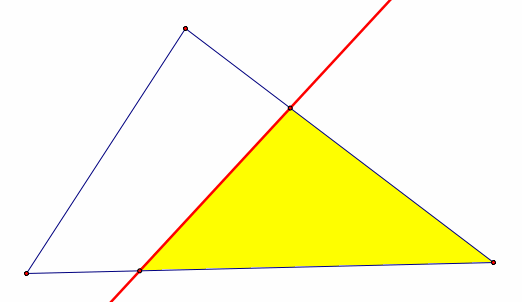
Construct a line through any selected point on AC to divide triangle ABC into two parts of equal area. Implement your construction with GSP, Investigate the construction, describe your construction, and prove that it is valid.
Construction by J. Wilson (GSP)
TRY THIS GSP. Run the animation.
Construction by Mike Walliser (GSP)
Construction by Brian Swanagan (requested)
Problem 4.3.6C (From me)
Construct a line through any selected point on AC to cut off a triangle of half the area of triangle ABC. Note: This allows for the selected point or the point of intersection with one of the other sides to externally intersect the side of the triangle. Investigate the construction, implement on GSP, describe your construction, and prove that it is valid.
TRY THIS GSP. Run the animation.
TRY THIS GSP. Run the animation.
TRY THIS GSP. Run the animation.
You might want to look at the following page from the EMAT 6600 web pages: Half the Area of a Triangle
Also, the following web paper, Trisecting the area of a Triangle, might be of interest.
