

Problem Set 4.5
Problem 4.5.1 See GSP File for solution by Jackie Ruff
In the figure, find the length of the indicated path from A to B in terms of r, the radius of the largest semicircle.
a. The first path is along the large semicircle with radius r
b. The second path is along the two semicircles, each with radius
c. The third path is along the four congruent semicircles
d. The nth path along
congruent semicircles
NOTE: The solutions given in the back of the text for parts b and c are in error.
Problem 4.5.2 See GSP file for solution by Cori Pringle
Imagine that a rope is tightly stretched around the Earth's equator. Assuming that the Earth is a perfect sphere, imagine that the rope is taken off and 100 feet are added to it. The extended rope is put back around the equator so that the "gap" created between the new circle and the equator is the same all around.
a) Without making any calculations, guess whether a cat could walk through the "gap" between the two circles.
b) Find the size of the "gap" -- that is, the distance between the two circles. Will the answer be different if the rope is stretched around the equator of a different planet?
Solution:
Problem 4.5.3 See GSP file for solution by Kathy Radford
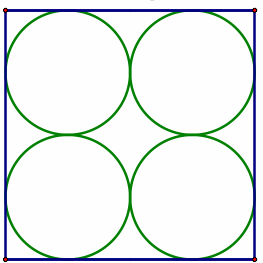
a. Four congruent circles are cut from a square sheet of tin as shown. What percentage of the tin is wasted?
Kathy observed that if a single circle is inscribed in a square, the ratio of the area of the circle to the area of the square is
. That is, the ratio of the area of a circle inscribed in a square to the area of the square is independent of the size of the square. It is always about 78.5 percent. So the waste is about 21.5 percent.
So the answer for parts a, b, and c of this problem is the same: regardless of the number of circles, the waste is going to be about 21.5 percent.
b. What percentage of the tin is wasted if nine congruent circles are cut out of the sheet?
c. What percentage of the tin is wasted if
congruent circles are cut out of the sheet?
Problem 4.5.4
For each of the following, find the ratio of the area of the outer circle circumscribing the regular polygon to the area of the inner circle inscribed in the polygon. (Note: Corrected statement of the problem.)
Problem 4.5.5.
Prove that the sum of the areas of the semincircles constructed on the legs of a right triangle equals the area of the semicircle constructed on the hypotenuse of the triangle.
Problem 4.5.6. See GSP File with Solution by Pei-Chun Shih
Triangle ABC is inscribed in a semicircle with diameter AB. With the legs of the triangle as diameters, two semicircles are constructed. Prove that the shaded area between the semicircles equals the area of the triangle.
Note: the area we want to show equal to the area of the triangle is the sum of the area of two lunes -- Lune ADCE and Lune CFBG
Note: A Lune is a concave plane figure bounded by two arcs of circles.
Also, you might want to examine the topic of Quadrature -- the construction of a square equal in area to some given area. For instance, since it is clear we could construct a square of the same area as the triangle above, it follows that we have a way of constructing a square with the same area as the sum of these two lunes.
If ABC was an isosceles right triangle, then we would be able to show the Quadrature of a Lune -- than is construct a square equal in area to a single lune. Since it is well known that we can not construct a square of the same area as a given circle, the quadrature of a lune (a figure made up of arcs of circles) is curious. In fact Hippocrates thought that the study of the Quadrature of the Lune would lead to a way for the Quadrature of the Circle. Much later it was demonstrated that there are exactly 5 special cases where the quadrature of a lune is possible.
Problem 4.5.8 See GSP File for Solution by Ken Montgomery
Each of the three congruent circles shown below passes through the centers
of the other two circles. Find the shaded area in terms of the radius r of the circles.
Problem 4.5.9 See GSP file for Solution from Nick Gomez
See my GSP File for one solution
In the regular hexagon with side a, six petals are drawn. Each petal is made of arcs of congruent circles whose centers are the vertices of the hexagon. All of the arcs intersect at the center of the hexagon (the center of the circumscribing circle). Find the unshaded area in terms of a. (Note I have changed the wording from the textbook because of difficulties of making shaded regions in the figure. In the book the region is shaded; here it is unshaded.)
Problem 4.5.10 See GSP file for Solution by Brian Swanagan
The four arcs in the interior of a square of side a are centered at the vertices of the square. Find the shaded area in term of a.
Problem 4.5.11 See GSP file for solution by Mike Walliser
Draw a circle and construct two new concentric circles that will divide the original circle into three non-overlapping regions of equal area.
See also GSP file from Nathan Wisdom for another solution.
Problem 4.5.12
In a circle, an arc that subtends a chord of length a is twice the length of an arc that subtends a chord of length b. Find the radius of the circle in terms of a and b.
Consider chord AB of length a. If the perpendicular bisector to AB is constructed from the center of the circle and extended to the circle at C, then chord AC is of length b. We can use Pythagorean relations to find an expression for r in terms of a and b.