L
Problem Set 5.1
1. Constructions
Perform Ml, the reflection of a point in a line, by
a. Paper folding
b. Paper Tracing
c. Mira
d. Compass and straight edge
e. GSP
2. a. Construct the image of a triangle ABC under reflection in a line l (with straightedge and compass). Describe your procedure and state the assumptions you are making in your solution.
3. Draw a Circle and a line that does not contain a diameter of the circle. Construct the image of a circle under the reflection in the line. Describe the construction in words and state any assumptions in your construction.
Note there are two situations to consider. Either the line intersects the circle or it does not. If your construction in Case 1 uses the assumption that the image circle and the given circle will intersect, then a different construction is needed for Case 2.
By definition, a reflection in a line is a transformation of the plane such the line is the perpendicular bisector of the segment PP' where P' is the image of P.
Thus in this problem, if O is the center of the circle, then the image O' will such that the segment OO' is bisected by the given line. Then since the radius of the circle is known, the image circle will be a circle with center O' with the same radius.
See GSP file from Victor Brunaud-Vega for a construction and discussion.
4. Line of Symmetry.
When the image of figure under reflection in a line is the figure itself, the line is referred to as the line of symmetry for the figure. For example, a rectangle has two lines of symmetry, each of which is the perpendicular bisector of the sides.
a. For each of the following figures, describe and draw all of the lines of symmetry of the figure. If the figure has no line of symmetry indicate that fact.
i. Segment. Two. The perpendicular bisector and the line along which the segment lies.
ii. Line. One. The line itself is a line of symmetry AND every perpendicular to the line is a line of symmetry!!!
iii. Square. Four
iv. Rhombus. Two.
v. Equilateral triangle. Three.
vi. Trapezoid. None.
An equilateral trapezoid will have one.
vii. Circle. An infinite number. Every diameter is a line of symmetry.
viii. Kite. One.
b. Find three figures not mentioned in part a and find their lines of symmetry
Isosceles triangle. One.
Scalene triangle. None.
Regular Pentagon. Five.
c. Describe the lines of symmetry of a regular n-gon. There are n lines of symmetry in a regular n-gon.
If n is odd, the there is a line of symmetry from each vertex perpendicular to the opposite side. n vertices, n lines of symmetry.
If n is even, the lines of symmetry are of two types. There are n/2 lines of symmetry connecting opposite vertices and there are n/2 lines of symmetry that are perpendicular bisectors of opposite sides. Total, n lines of symmetry.
d. How many lines of symmetry can an n-sided polygon have if it is not necessarily regular.
For TRIANGLES, we have seen the scalene triangle has 0 lines of symmetry; the isosceles triangle has 1 line of symmetry, and the equilateral triangle has 3 lines of symmetry. 0, 1, and 3. Is it possible to have a triangle with two lines of symmetry? Why not? Can a triangle have more that 3 lines of symmetry.
For QUADRILATERALS, clearly we could have a four sided figure with four sides of different length and it would have 0 lines of symmetry. We have seen a trapezoid with 0 lines of symmetry. A kite has 1 line of symmetry as does an isosceles trapezoid. How many lines of symmetry in a parallelogram that is not a rhombus or rectangle? The rhombus and the rectangle have two lines of symmetry. The square has 4 lines of symmetry. Is there any quadrilateral with 3 lines of symmetry? Is there any quadrilateral other than the square that has 4 lines of symmetry?
For a 15 sided polygons, what are the possible number of lines of symmetry? Can you construct examples? Clearly it is easy to construct a 15 sided figure with 0 lines of symmetry, or one with 1 line of symmetry, or a regular figure with 15 lines of symmetry. What other numbers are possible? Construct examples.
For n-sided polygonal figures what are the possible number of lines of symmetry other than 0, 1, and n?
Is having n lines of symmetry a necessary and sufficient condition for a polygon to be regular?
5.
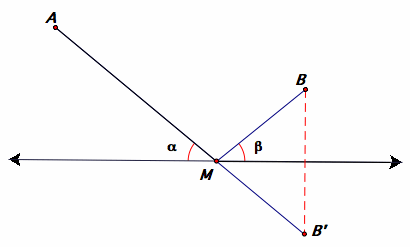
When a ray of light bounces off a surface, or when a billiard ball bounces off the rail of a billiard table, the angle between the surface and the incoming ray equals the angle between the surface and the reflected ray. That is, alpha = beta in the following figure. Assuming this fact, show the following:
a. Prove that the path the light will travel from a source A to a mirror surface x and then to B can be obtained as follows:
Find B', the reflection of B in x. The intersection of segment AB' with line x is the required point M on x.
Solution: My e-mail suggests there may be some confusion about what is to be proved. We need to prove that the construction leads to a point M such that the angle of incidence equals the angle of reflection. We are not given the point M.
b. Prove that the path A-M-B is the shortest path connecting point A to a point on x to a point B. That is, show that if M1 is any point on x such that M1 ≠ M, then AM1 + M1B > AM + MB. [Hint: use your answer from part a and the triangle inequality.]
Solution: Here we need prove that the point M constructed in Part a where angle of incidence equals angle of reflection leads to the shortest path. Construct a point M1 on x such that M1 ≠ M. Construct AM1, M1B, and M1B'. Now consider triangle AM1B'.
c. Let the line through M be the x-axis. If the coordinates of A and B are (x1, y1) and (x2,y2) respectively, find M (x, 0) in terms of A and B.
There are many ways to set this up. Perhaps a most straightforward is to observe that M is on AB' and so the slope of AB' is the same as the slope of AM.
See GSP file for solution from Jackie Huff
See GSP file for similar solution and discussion
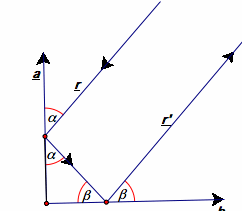6.
Consider a ray of light bouncing off two perpendicular surfaces show in the following figure.
a. Draw two perpendicular lines a and b, choose an initial ray r, and construct (using any tools) outgoing ray r'. Repeat your construction for different angles that the ray r makes with line a, and in each case construct the outgoing ray r'. State a conjecture concerning the relationship between r and r'.
Construct the configuration with GSP and build an animation of the angle for r. Click HERE.
The most obvious conjecture is that r and r' lie on parallel lines.
b. Prove the conjecture in Part (a).
Proof: We use the isometries Ma and Mb
See GSP File from Laura Singletary
The conjecture could also be proved using rotations as the isometry transformations.
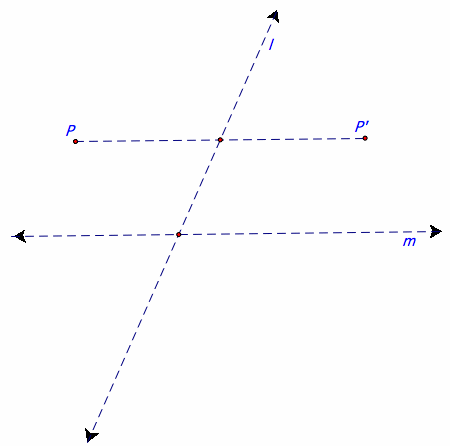Problem 5.1.7. In Example 5.1, we defined a transformation F using lines l and m as follows: /any point on l is mapped onto itself; if a point P is not on l, its image P' is such that PP' is parallel to m and bisected by l. The lines l and m were nonperpendicular.
7a. We have shown F is not an isometry in Example 5.1; that means it is not always true that PQ = P'Q'. However, the transformation pay preserve the distance between certain points. Do any such points exist? If so describe them and justify your answer.
Hint:
Consider points P and Q that would be their own self image.
Consider points P and Q on a line parallel to m
Consider points P and Q on a line parallel to l
See GSP File from Jackie Huff for a a solution.
7b. Prove that F does not preserve equality of distance. That is, if PQ and RS are two segments of equal length, show that it is not always the case that P'Q' = R'S'. (Hint: construct a counterexample.) Note that equality of distance is more than the test of isometry; We need to show that congruent segments will not necessarily map to images that are congruent segments.
See GSP file, page 2, for a Solution to 5.1.7.b
The counterexample shown here is to let RS be PO, choosing PO as a segment with is invariant under F. Then PQ is constructed of the same length as OP. The image of PQ is PQ' and the image of PO is PO. Assume that the images are of equal length. This forces triangle POQ to be isosceles and this leads to a contradiction.
7c. Does the transformation preserve the midpoints of segments? That is, if M is the midpoint of segment AB, is it always the case that M' is the midpoint of segment A'B'? Either prove this statement or show a counterexample.
The statement can be proved; the midpoint is preserved under transformation F.
Construct AB and its midpoint M. Find the images A', B' and M'
A trapezoid is formed with AA' parallel to BB'
M is given as the midpoint of AB and MM' is parallel to AA' and BB' by the transformation F. By parallel projection M' is the midpoint of A'B'
7d. Does the transformation F preserve parallelism? That is, is it true that whenever two lines are parallel, their images are also parallel? Either prove this segment of give a counterexample.
Proof that Parallelism is preserved:
Construct line r with segment AB and and line s with segment CD with AB = CD so that a parallelogram is formed.
Find the images A', B', C', and D'.
Construct diagonals AC and BD
Because ABCD is a parallelogram by construction, the diagonals intersect and M and bisect each other.
By part c we have shown that the midpoint is preserved under F
So the image M' of M under F will be the midpoint of A'C' and B'D'. Therefore the diagonals of the image A'B'C'D' bisect each other and so A'B'C'D' is a parallelogram.
Thus parallelism is preserved under transformation F. See GSP file for details of the solution.
7e. Prove that the transformation preserves the area of a triangle.
Proof:
Consider Triangle ABC with AB Parallel m
Take image Triangle A'B'C' under F.
From Part a we know that AB = A'B'
So the triangle and its image triangle will have the same lengths bases and the same lengths altitudes. Therefore area is preserved.
To consider the case when AB is not parallel to m, divide the triangle into two parts.
See the GSP file for the solution details.
7f. Does the proof in 7e imply that the transformation F preserves the area of any figure? Justify your answer.
Yes, any plane figure.
a. Any polygonal figure can be subdivided into triangular regions. Since 7e shows area is preserved for triangles, then it must be preserved for polygonal regions as well.
b. For non-polygonal figures, polygons can be used to approximate the area inside and out as we did for the circle.
7g.
7.h. Richard
8. Prove that a function from the plane to the plane that preserves distance is a transformation of the plane and hence an isometry
9. Prove the six properties of isometries listed on page 244.
1. If A and B are any two points and A' and B' are their respective images, then A'B' = AB.
Given, in the definition.
2. Isometry preserves collinearity. That is, if A, B, and C are collinear, so are their respective images A', B', and C'.
Proof:
If A, B, and C are collinear, and B is between A and C. Then AB + BC = AC.
Isometries preserve distance, so A'B' + B'C' = A'C'.
By the triangle inequality, therefore, B' is on A'C'.
3. The image of a line is a line and the image of a segment is a segment.
Proof:
Suppose line k is given with points A and B and we have an isometry T. The image point A' and B' will determine a line m. We need to show that every point on k has an image point on m and every point on m is an image of some point on k.
Pick any point P on AB. By Isometry Property 2 then T(P) is on m and collinear with T(A) and T(B).
Now, suppose Q is a point on m. Q, T(A), and T(B) are collinear. The inverse of T is also an isometry.
Again by using property 2, the images of Q, T(A), and T(B) are collinear and since A and B are on k, then Q is on k.
The proof that the image of a segment is a segment is similar. The points of a segment AB are those points that lie between A and B on the line AB. The proof of Isometry Property 2 has established betweeness.
4. The image of a triangle is a triangle congruent to the original triangle.
Proof:
Triangle ABC under an isometry maps to an image triangle A'B'C'. Since isometries preserve distance, then AB = A'B', AC = A'C', and BC = B'C'. Therefore by SSS triangle ABC is congruent to triangle A'B'C'.
5. The absolute value of angle measure is preserved: The absolute value of the measure of the image of an angle equals the absolute value of the measure of the angle.
Proof:
By Isometries Property 4, and an isometry maps a triangle ABC to a congruent triangle A'B'C'.
Since the measures of corresponding angles of congruent figures are equal, the angle measure is preserved under the isometry.
6. Betweeness is preserved: If A - B - C (B is between A and C), then A' - B' - C'.
Proof: This is an immediate consequence of Isometry Property 2, above.
10. a. Use tracing paper to find a point P under a translation from M to N.
The process is to point P on the tracing paper and lay it over a drawing of the vector MN. Then locate P'.
b. Use the properties of a parallelogram to construct TAUMN(P). Explain your procedure and prove that it works.
See the GSP file from Karyn Carson for one solution.
We are given three point M, N, and P and are to construct the a parallelogram MPP'N.
c. Find TAUNM(TAUMN(P)). What does the result tell you about TAUNM º TAUMN?
See the GSP file from Karyn Carson for one solution and proof.
We have encountered a previous exploration of composition in Now Solve This 5.2.
d. Base on the answer to Part c, what is the inverse of TAUMN?
See the GSP file from Karyn Carson for one solution and proof.
11. Classify each of the following statements as true or false. If the statement is true, prove it. If it is false give a counterexample.
a.
º
is a translation.
b.
is a translation
c.
All of these are true. See the GSP file from Kathy Radford for discussion and proof.
12. Kathy
14. Treasure Island Problem, Chapter 0 and also Problem 1.3.37.
See solution and discussion in GSP file by Allyson Hallman
Also, see Island Treasure Problem from the EMAT 6600 Problem Solving page.
Also, this problem was in the final examination pool for the set of items. Several of you presented solutions.
I think Professor Libeskind is trying to introduce different approaches, different geometry tools, for exploring this problem in various ways. Here he is trying to lead us to seeing the use of rotations to show that locating the gallows at two different locations will mean that the analysis leads to the same spot for the treasure. Since one of the locations is selected arbitrarily, then we can conclude that the treasure is in this spot regardless of where the gallows is located.
17. Which of the following mappings F from the plane to the plane are transformations? Which are isometries?
a. The mapping in equation a is a translation with vector OP defined by the points (0,0) and (0,1). We have parallelogram OPK'K.
b. The mapping in equation b is a translation with vector OP defined by the points (0,0) and (-1, 1). We have parallelogram OPK'K.
c. Not a transformation. Why?
d. Not a transformation. Why?
e. Not a transformation. Why?
18. Nick
19.
Laura has use the example when R = 3.5, h = 10 and k = -4 to illustrate the problem.
If we have a transformation (x,y) to (x + h, y + k), this means that from the definition of a translation, the vector from A(0, 0) to B(h, k) is used to construct an image point from P(x,y) by a parallelogram with two of the sides being AB and PP'
Thus the center of the circle is mapped to the center point of the image circle by the vector AB and any point (x,y) on the circle is mapped to its image point (x',y') = (x + h, h + k).
20. Doug
21. Recall that a curve is said to have line symmetry if its reflection in the line is the curve.
It has rotational symmetry if the image under the rotation is the curve itself.
It has translational symmetry if the image of the curve under the translation is the curve itself.
Find all of the symmetries of the following curves and justify your answers. See GSP file for solutions by Amberly Roberts
Graph of a. Graph of b. Graph of c. Graph of d.
Graph of e. Graph of f. Graph of g. Graph of h. Graph of i.
24. Consider all lines y = ax + b. Which of these lines have the line y = x as their line of symmetry.
