

Problem Set 5.4
Problem 5.4.1 See GSP File for one construction
Problem 5.4.2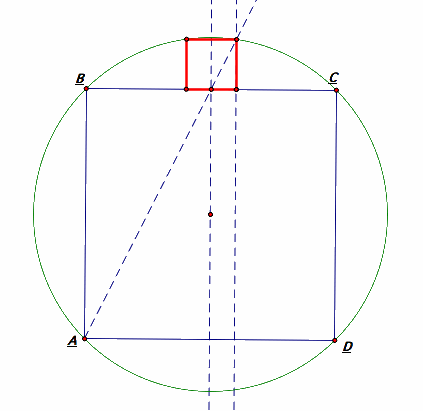
a. In a given circle, inscribe a square ABCD and a smaller square EFGH with two vertices on the arc BC and the other two vertices on side BC.
b. If the side of the larger square is x, find the side of the smaller square in terms of s.
Problem 5.4.3 Click here for a GSP file with this solution. Or, Click here for a solution by Mike Walliser. Mike's solution has a different implementation of the ratio that is used in the dilation.
A solution will not exist if a circle with center on b and tangent to a does not intersect line c.
Problem 5.4.4
Problem 5.4.5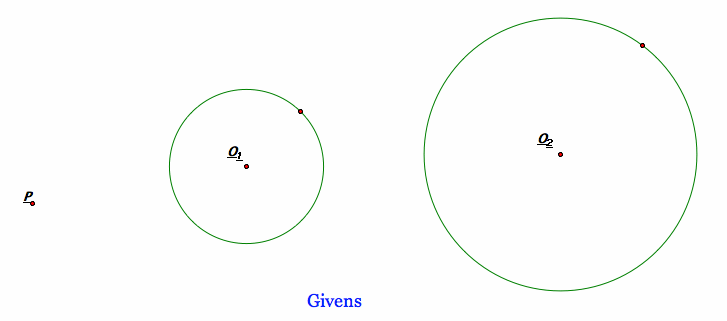
Two circles with centers O1 and O2, respectively, and a point P are given. Construct a circle with center X (not known) such that the line through A and B, which are the points of tangency (of each of the circles with the unknown circle), contains the point P.
There is still a need to prove this construction solves the problem. Assume you have the two given circles and the tangent circle with A and B as the points of the respective tangencies. The line AB would also intersect each of the given circles at R and S, respectively, creating isosceles triangles RO1A and BO2S. The circle tangent to A and B with center at X would also have an isosceles triangle AXB. Furthermore, O1, A, and X are collinear as O2, B, and X. The three triangles are similar. Therefore, the dilation from O, the center of similitude for the two given circles, would map triangle RO2A onto triangle BO2S and therefore the line AB contains point O.
Thus if OP intersects the two circles, the intersection points A and B will determine the tangent points for the circle with center X.
Problem 5.4.6 A GSP file for this solution is available.
Through a point in the interior of a given circle, construct a chord that is trisected by the point.
Is it possible to construct such a chord for any point P in the interior? If not, what is the region of the circle where the point P can be located?
Given a circle with interior point P.
Suppose we had the desired segment AB. If a dilation with center P had a ratio of -2, the point A would be mapped to an image located at B.
The image of A would also be on an image circle with radius twice the size of the given circle and center on the line from the center of the given circle but on the opposite side of P and twice the distance from P.
We do not know the location of A or B but we might be able to see the intersection of the given circle and the image circle.
So for the construction, we take P as the center of a dilation with radius -2 and find the image of the given circle.
The intersection of these two circle is the longer end of our segment from P.
We complete the construction with a chord along the line of P and the intersection point.
Proof:
Point B is on both circles. It is the image of some point on the given circle and thus PB is twice the distance as P is from the point on the given circle for which B is the image. But that point is on the line PB. Therefore AB is the chord that satisfies the conditions.
When is this construction not possible? Clearly, if the image circle under the dilation does not intersect the given circle, then no image point is determined.
Open the GSP file and drag point P in the construction to get a sense of when it will not work.
When P is near the center of the given circle, there will be no intersection. In fact if the distance of P from the center of the given circle is 1/3 of the radius, the image of the center will be on the given circle, the radius of the image circle will be the diameter of the given circle and so the image circle will be tangent to the given circle. In this special case, the chord would be a diameter and P would be a trisection point of the diameter as well as a trisection point of the radius.
If the distance of P from the center is less than 1/3 the radius, the chord does not exist.
Problem 5.4.8
Are all parabolas similar to each other? Justify your answer.
Problem 5.4.9
Problem 5.4.10
Are all hyperbolas xy = c, where c is any real number, similar to each other? Justify the answer.