

Overview of Section 1.3 The Parallel Postulate and Its Consequences
Euclid's Fifth Postulate -- the Parallel Postulate
If a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which the angles are less than the two right angles.
Playfair's Axiom is one of many equivalent statements for the Parallel Postulate:
Axiom 1.2 The Parallel Postulate (Playfair's Axiom): Given a line and a point not on the line, there exists a unique line through the point parallel to the given line.
Althought it is not clear to everyone that Playfair's Axiom and the Euclidean Fifth Postulate are "equivalent" it is worth some effor to understand. Playfair's axiom seems much simpler and easier to use. We are going to accept the statement of equivalence rather than construct a proof of it.
Theorem 1.18: (Converse of Theorem 1.17) If two parallel lines are cut by a transversal, then a pair of corresponding angles is congruent.
The proof of Theorem 1.18 provided in the text is very straightforward and easy to follow.
In Theorem 1.17 congruent corresponding angles, means the lines are parallel.
In Theorem 1.18, parallel lines, means the corresponding angles are congruent.
To prove Thm 1.18 with an indirect proof we assume a pair of corresponding angles is not congruent (e.g. angle 1 and angles 2). Then there must be another line through P with a corresponding angle congruent to angle 1.
The result applies to all pairs of corresponding angles. (see page 36).
Theorem 1.19: Two lines in a plane are parallel if and only if a pair of corresponding angles formed by a transversal is congruent.
Is Theorem 1.1.9 essentially a restatement, in the "if and only if" language, of Theorem 1.17 and Theorem 1.18? If not, how is it different?
Theorem 1.20: Two lines in a plane are parallel if and only if a pair of alternate interior angles formed by a transversal is congruent.
Proof:
1. Given two lines are parallel. By Theorem 1.19, a pair of corresponding angles are congruent. If one of the corresponding angles is an interior angle, then its corresponding angle is the vertical angle of the other alternate interior angle in the pair. Therefore the alternate interior angles are congruent.
2. Given a pair of alternate interior angles is congruent. Then a corresponding angle to one of the angles in the pair is a vertical angle which is congruent each of the two alternate interior angles. Therefore by Theorem 1.19 the lines are parallel.
Theorem 1.21: Two lines are parallel if and only if a pair of interior angles on the same side of the transversal is supplementary.
EXAMPLE 1.5
Now Solve This 1.9
1. Find an expression for the sum of the measures of the interior angles of a convex n-gon in terms of n.
Hint: Construct the diagonals of the convex n-gon from one of the vertices to create non-overlapping triangles.
2. What is the sum of the measures of the Exterior angles of a convex n-gon. Prove your answer.
Theorem 1.23: A Saccheri quadrilateral is a rectangle.
DEFINITIONS
Trapezoid -- a quadrilateral with at least one pair of parallel sides
This is the most widely accepted definition of a trapezoid in mathematics literature. Some folks get very uptight about a different definition (EXACTLY one pair) they have learned. Whatever definition is chosen, you follow the logical implications of it. With this definition, rectangles, parallelograms, and rhombuses would all be special cases of trapezoids. In other parts of the world, this figure may be called a trapezium rather than trapezoid.
Parallelogram -- a quadrilateral in which each pair of opposite sides parallel.
Rhombus -- a quadrilateral with four congruent sides; or, a parallelogram with a pair of adjacent sides congruent.
Square -- a rhombus with a right angle
Rectangle -- a parallelogram with a right angle.
Lemma: A rectangle is a quadrilateral with four right angles.
Theorem 1.26: In a parallelogram:
1. Each diagonal divides the parallelogram into two congruent triangles.
The other half of the proof when diagonal AC is used to show triangle ABC is congruent to triangle CDA is constructed in the same manner but will not be produced here.
2. Each pair of opposite sides is congruent.
Proof: This result follows immediatly from the result in Part 1. The opposite sides of the parallelogram are corresponding parts of congruent triangles.
3. The diagonals bisect each other.
Theorem 1.27:
1. A quadrilateral in which each pair of opposite sides is congruent is a parallelogram.
2. A quadrilateral in which the diagonals bisect each other is a parallelogram.
3. A quadrilateral in which each pair of opposite angles is congruent is a parallelogram.
4. A quadrilateral in which each pair of opposite sides is parallel and congruent is a parallelogram.
Now Solve This 1.10
1. Prove Theorems 1.24 through 1.27.
2. Theorem 1.27 (4 parts) rephrased in "necessary and sufficient condition" language
1. A quadrilateral is a parallelogram if and only if each pair of opposite sides is congruent.
2. A quadrilateral is a parallelogram if and only if the diagonals bisect each other.
3. A quadrilateral is a parallelogram if and only if each pair of opposite angles is congruent.
4. A quadrilateral is a parallelogram if and only if each pair of opposite sides is parallel and congruent.
Construction 1.5: Construction of a line through P (not on l) Parallel to l.
Essentially, with P as one vertex and one side on the line, construct a parallelogram (or rhombus).
Parallel Projections
Vertical projection -- along a perpendicular
Projection of P in any direction
Projection of P on parallel
Projection from a line k to a line l in the direction of m
Theorem 1.29: A parallel projection preserves congruence of segments belonging to the same line
A proof is provided in the text but I am recreating it here because I think there is an error in marking the figure. This theorem says that if we have two congruent segments on one line, then under a parallel projections, the images on another line are congruent. It helps to remember that the parallel projection is from one transversal to another.
The proof considers two cases.
In Case 1, the two transversals are parallel:
We can use this result in the proof for Case 2:
Case 2: The transversals l and k are not parallel.
Remember, the parallel postulate indicates there is exactly one parallel to a line through any point not on the line.
The parallel projection is pictured here.
If we are given that AB = CD, we want to prove A'B' = C'D'.
We use the result from Case 1 mapping points from line k back to lines parallel to k but intersecting l. Such a line maps A'B' to AE and C'D' to FG.
We know that A'B' = AE and C'D' = FG and in the same way we have C'D' = CH. We need to show that AE = CH
Consider the triangles ABE and CDH. We are given AB = CD. Because l is a transversal, the angle at B and the angle at D are congruent. Also the angle at A and the angle at C are corresponding angles. Thus by the ASA congruency condition, the triangles ABE and CDE are congruent. From this we know that AE = CH and therefore A'B' = C'D',
Corollary 1.6: If three or more parallel lines intercept congruent segments on one transversal, then they intercept congruent segments on any other transversal.
If AB = BC = CD = DE = EF = FG, then the corresponding image segments are congruent.
Construction 1.6: Division of a segment into any number n of congruent parts.
The contruction follows from the corollary. Take the segment to be divided to lie along one transversal. Construct a second transversal through one end of the segment and mark on n congruent and adjacent segments on the second transversal. Construct a parallel projection from the second to the segment you wish to divide, using the other end of the segment to determine the parallels for the projection.
Now Solve This 1.11
We have seen that the diagonals of a parallelogram bisect each other. Suppose they bisect each other at O.
1. If we draw a line through O and it intersects two parallel sides of the parallelogram at points P and Q, respectively, prove that OP = OQ
Proof:
The diagonals of a parallelogram bisect each other. So a line through O parallel to the parallelogram sides containing P and Q will give a parallel projection from one transversal to another. From each diagonal being a transversal we know that in this case the parallel projection cuts off congruent segments. Therefore in cuts off congruent segments on PQ and PO = OQ.
2. The statement in Problem 1 is a generalization of a fact stated in the proof of Theorem 1.29. Which fact? Why is Problem 1 a generalization of the fact?
The parallel projection maps congruent segments to congruent segments on all other transversals.
Medians of a Triangle See Centroid
Now Solve This 1.12
Alternative proof that any two medians intersect at a point that divides each median into segments whose lengths are in a ratio 2:1.
Example 1.6
What kind of quadrilateral is obtained when the midpoints of consecutive sides of the quadrilateral are connected? See GSP file.
Prove that the resulting figure is a parallelogram
Given quadrilateral ABCD with midpoints of the sides at E, F, G, and H. Construct quadrilateral EFGH.
Construct diagonals AC and BD.
By the Midsegment Theorem, GH is the midsegment for triangle ABD and parallel to BD. EF is the midsegment for triangle CBD and parallel to BD.
Therefore HG is parallel to EF
HE is a midsegment for triangle ABC and parallel to AC. GF is a midsegment for triangle ADC and parallel to AC.
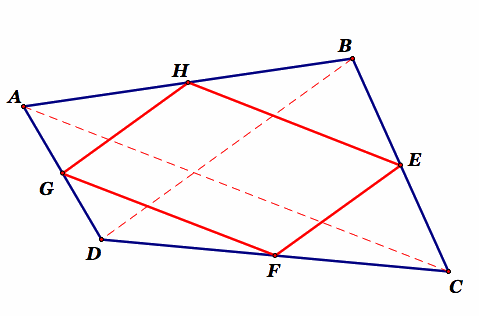
Therefore HE is parallel to GF.
Two pairs of parallel sides means the quadrilateral is a parallelogram..
We would also know that the respective lengths of the sides of the parallelogram were one-half the length of the parallel diagonal.
Does the quadrilateral have to be convex?
Open the GSP file and drag a vertex to explore.
What if the quadrilateral is not a simple closed figure, but 'crosses itself?'
Open the GSP file and drag a vertex to explore.
Do the vertices of the quadrilateral for any of the above need to be in the same plane?
Example 1.7
Exploration of when the parallelogram in Example 1.6 is 1) a rhombus or 2) a rectangle.
Use the GSP file to explore. The image shows a case where MNPQ is a rectangle.
Example 1.8
1. State and prove the Midsegment Theorem for trapezoids.
2. Prove that the segment connecting the two midpoints of the diagonals of a trapezoid is parallel to the bases of the trapezoid and find the length of this segment if the bases are of lengths a and b. Open GSP File to explore.
SEE PROBLEM 1.3.20 -- Has this proof covered what is missing in the proof contained in Problem 1.3.20?
Now Solve This 1.13
Treasure Island Problem