

Overview of Section 4.4 The Golden Ratio and the Construction of a Regular Pentagon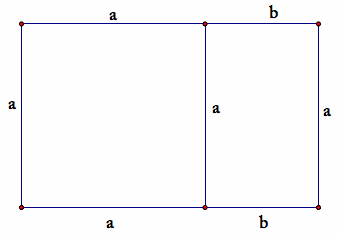
Definition: Golden Rectangle
A golden rectangle is a rectangle with the property that if it is dissected into two pieces -- a square and a rectangle -- then the new rectangle is similar to the original rectangle.
NOTATION --
Although it will make no difference in determining the common ratio of the sides of the two rectangles, I have chosen to label the first with length a + b and width a while the second is length a and width b. Note the image to the right.
The definition, with this terminology, gives the equation
.
is called the GOLDEN RATIO or the Divine Proportion.
The Sublime Triangle
The Sublime Triangle is an isosceles triangle with base of length a and angles of measure 72, 72, and 36. If you construct the angle bisector of one of the base angles, its intersection with the opposite side divides the sublime triangle into two similar triangles by the AA similarity conditions. Let the base of the smaller triangle be b and therefore the lengths of the two sides of the sublime triangle are each a + b.
Therefore the ratio of the side of the sublime triangle to its base is the golden ratio.
I prefer to introduce the Golden Ratio via the Sublime triangle and use the similarity of the triangle rather than using the Golden Rectangle and similarity of rectangles. I think it is easier to understand and less prone to errors of labels and fuzzy notions of similarity about rectangles.
Problem 4.4.1 asks to prove that the ratio of the longer side to the shorter side of the Sublime Triangle is
.
The Pentagon and the Sublime Triangle: Not that if the obtuse triangle with sides a, a, and a + b is reflected the longest side, and the corresponding construction is done on the other side, a regular pentagon is produced. The sides of the pentagon are of length a and the diagonals are of length a + b. This observation leads to many theorems and relationships about pentagons as well as a strategy for constructing a pentagon.
Dividing a line segment AB into two parts AC and CB such that the ratio of the two parts is the Golden Ratio
If we have any segment AB, we can do a construction to locate such a point C in the following way by considering
This is a fundamental construction. I suggest you create your own GSP File and Script tool for drawing a segment divided into two segments in the ratio of the Golden Ratio. From this tool, it is relatively simple to
a. Construct a Golden Rectangle (Construction 4.1)
b. Constrict a regular pentagon given a side. (Construction 4.2)
c. Construct a regular pentagon given a diagonal.
d. Construct a regular pentagon given the radius from the center to a side.
e. Construct a regular decagon. (Now Solve This 4.13)
Here is a construction for partitioning segment AB. This can also be seen step by step in the GSP file for GoldenAB. It is strongly suggested that you make your own GSP file for this construction and find a way to do each of the 5 constructions listed above. This construction for partitioning the line segment in the Golden Ratio is Now Solve This 4.12 and Problem 4.4.2.