Comments on the Problem:

Multiple Solutions

By

J. Wilson

Find as many solutions as possible for A, B, and C that satisfy both equations:

ABC = 4

and

3A + 2B - C = 3

What observations can you make about your results?

Graph the two equations with NuCalc 2.0 or Graphing Calculator 3.0. You will have to use equations with x,y, and z as the variables, rather than A, B, C.

In this picture the blue surface comes from ABC = 4. It is in four separate parts. The red surface is a plane determined by the equation 3A + 2B — C = 3. The plane intersects three of the separate parts of the blue surface.

You need to see your own graph, allow it to turn slowly to see it from several angles, and zoom out or zoom in to see the appropriate part of the surfaces.

Solutions we seek would be on intersection of the red plane with the blue surface. There can be solutions where all three values are positive -- that set of solutions seems to lie along a curve shaped like a parabola.

Further, we can see from the graph that if C is positive, then any solution will also have A and B positive.

If C is negative, then one of A or B is positive and the other is negative.

Can you infer these two observations from the equations?

Reduce the graph to a two dimensional graph. For example, set C to some constant and consider the graphs

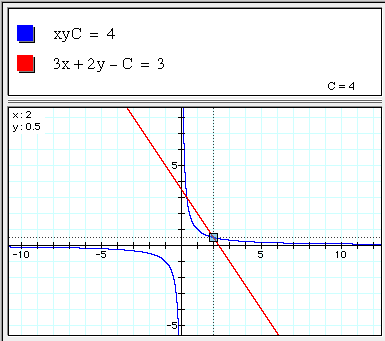
xyC = 4

3x + 3y — C = 3

Where the two graphs intersect will be a solution for that value of C. Note, NuCalc or Graphing Calculator will begin with the default value of C = 1. Type in the equations just as given here, using the letter C. Repeat for several different values of C. Here is the case for C = 4. One solution is A = 2, B = 0.5, C = 4.

RETURN

Do not forget to look at negative values of C and values of C that are not an integer.

EXTENSION:

Would this problem require a different approach if the solution asked for only integers for A, B, and C?