Part 1: Some thoughts on thinking about mathematical knowledge
for secondary mathematics teachers
We began
our consideration of the question in terms of goals and thoughts about those
goals.
Goal: To
characterize the mathematical knowledge that is needed by secondary mathematics
teachers (SMTs).
Characterization of mathematical knowledge for SMTs
requires responses to each of the following:
What are the ways of thinking about mathematics with which
SMTs should be familiar?
What are the mathematical understandings, skills, and
dispositions with which SMTs should be familiar?
What are the understandings of the nature of mathematics
that SMTs should have?
[What are the ways in which SMTs should understand their
students’ mathematical thinking? – is this mathematical knowledge?]
One way
to think about responses to questions like these is to think about the
mathematical knowledge required in the work in which SMTs engage.
How
will SMTs be called upon to draw on mathematical knowledge? Following are some
of the ways:
Š
Deciding
on what mathematics is important for students to learn– wrt the goals of
an entire mathematics program – wrt the possible futures of their
students. This requires (among other things):
o
Identifying
mathematical ideas that cut across school mathematics
Š
Developing
units and lessons that sequence and develop important mathematics –
taking into consideration the connections among topics. This requires (among
other things):
o
Identifying
appropriate ways in which school mathematics can be structured to facilitate
its use in further endeavors (work?) and its development in later mathematics
Š
Responding
to students’ mathematical questions:
o
Choosing
from among a large range of possible representations and explanations. This
requires (among other things):
§
Seeing
the mathematical objects in external representations
§
Understanding
what various representations of a mathematical object conceal and what they
reveal
o
Capitalizing
on opportunities to help students see connections across mathematical areas.
This requires (among other things):
§
Understanding
the generalizations and principles that connect mathematical ideas in the
school mathematics curricula
§
Š
Constructing
assessments of student understanding.
How might we as a field begin to answer questions like
these[1]? In order to make progress on
understanding the mathematical knowledge that is needed by secondary
mathematics teachers (SMTs), we need to draw from both mathematics and
practice. We want teachers to be flexible enough in their mathematical
knowledge to recognize those classroom opportunities to make connections to
other mathematics, to create foreshadowing of ideas to come, and to identify
and build toward “big ideas” in mathematics. We have developed a rough plan to
start on the road to developing those ideas. The plan builds from vignettes
based on classroom practice. We have two sketches of examples of vignettes.
Sample
Vignette 1:
The first example of a vignette arose from talking about Pat’s
recent observation in a high school classroom. The student teacher Pat was
observing had just completed a discussion of special right triangles, including
(of most interest here) discussion of the 30°-60°-90° triangle. Discussion then turned to right
triangle trigonometry, with the teacher showing the students how to calculate
the sine of various angles using the calculator. A student then asked how he
could calculate sin (32°) if he did
not have a calculator. The student teacher was stymied. Pat’s observation was
that the student teacher could have made a good estimate of sin (32°) by returning to what he had just taught
about the 30°-60°-90° triangle. The point is that there are lots of
mathematically appropriate responses to this student question, and that
teachers ought to be able to generate those responses and choose from among
them. In this case, the student teacher, under some circumstance, might use
this as an occasion to begin discussion of the trig functions as defined on a
unit circle. With a carefully drawn (also large and legible) unit circle, the
student could find an estimate of the sine of any angle. The student could be
drawn into thinking about the unit circle as a trig “calculator,” and of the
sine as a function defined on a continuous interval (not those words , but that
idea). And so on…
Sample
Vignette 2:
A second example comes from Rose Zbiek’s work with
parametric GSP drawings. This example, appearing in CAS-Intensive Mathematics
(Heid and Zbiek, 2004)[2], was inspired
by a student mistakenly grabbing points representing both parameters (A and B
in f(x) = Ax + B) and dragging them simultaneously (the difference in value
between A and B stays constant). This generated a family of functions that
coincided in one point. Interestingly, no matter how far apart A and B were
initially, if grabbed and moved together, they always coincided on the line x = -1.
See Figure 1 for a screen dump after A and B have been simultaneously
dragged. Rose then thought to
generate an extension to quadratic functions (which also appears in
CAS-Intensive Mathematics).
Because of her mathematical understanding, Rose was able to recognize
the potential of this accident for making mathematical connections –
first from the graphical phenomenon to a symbolic proof and then to extend this
exploration to a polynomial of higher degree (which generated another
interesting relationship along with its proof). In this case, GSP was a vehicle
that brought mathematical relationships to the fore. Seeing the phenomenon is
not enough – teachers need to recognize the potential for mathematics in
the patterns they see.
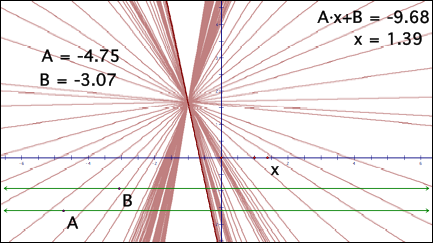
Figure 1. Screen dump showing trace of f(x) = Ax + B after A and B have been dragged simultaneously.
These
two examples are limited in several ways: they both arise from unanticipated
student actions, and they are not necessarily common occurrences in the
mathematics classroom. The set of examples could be expanded in several ways.
First, the examples might include instances of situations in which teachers
need to call on their mathematical knowledge without being prompted by a
student action. For example, teachers might need to call on their mathematical
knowledge in creating new ways to develop a lesson or unit or in creating
assessments or assignments for their students. Second, the examples might
include more common classroom occurrences. Examples were provided by a seminar
of University of Georgia doctoral students. Ones by Bob Allen and Dennis
Hembree follow.
Example 1: A teacher is teaching about factoring perfect
square trinomials and has just gone over a number of examples (e.g., ![]() ).
Students have developed the impression that they need only check that the first
and last terms of a trinomial are perfect squares in order to decide how to
factor it. They are developing the impression that the middle term is
irrelevant so that
).
Students have developed the impression that they need only check that the first
and last terms of a trinomial are perfect squares in order to decide how to
factor it. They are developing the impression that the middle term is
irrelevant so that ![]() no matter what the term in the box. The
teacher needed to construct a counterexample on the spot, and he wanted one
whose terms had no common factor besides 1. What mathematical knowledge did he
did to accomplish his task?
no matter what the term in the box. The
teacher needed to construct a counterexample on the spot, and he wanted one
whose terms had no common factor besides 1. What mathematical knowledge did he
did to accomplish his task?
Example 2: A teacher
is intending to illustrate how to solve three linear equations in three
unknowns and has written the
following on the board: ![]() .
Before the teacher can write the third equation, the student asks, “What if you
have only two equations?” What options does the teacher have to respond to the
student’s question and upon what mathematical knowledge would the teacher have
to draw in order to respond in those ways?
.
Before the teacher can write the third equation, the student asks, “What if you
have only two equations?” What options does the teacher have to respond to the
student’s question and upon what mathematical knowledge would the teacher have
to draw in order to respond in those ways?
Vignettes
like these can help us think about the mathematical knowledge needed by
secondary mathematics teachers. Here are steps of a potential plan for creating
and using these vignettes to assist us to understanding the nature of the
mathematics for secondary teachers.
1.
Activity: Generate
some good sample vignettes. We need to create some and send them back and forth
for feedback to refine them. One question is who would generate them–perhaps
groups at each of the institutions could generate some. Whatever the process,
we could coordinate that production and feedback cycle once we find out who is
interested. One by-product of this process could be the development of
guidelines for the creation of vignettes. [Should they be descriptions of the
incident or problem being addressed? Should they include development of the
mathematical responses and of the mathematical knowledge needed to create those
responses?] Resources that might provide some ideas for these vignettes include
Mathematical questions from the classroom by Richard Crouse and Cliff Sloyer and Situations in Teaching, by Alan Bishop and Richard Whitfield.
Timeline: To
occur between now and the end of May. This will require sending drafts back and
forth until we get a consensus on what we want these vignettes to look like.
2.
Activity: a. Generate
vignettes at the Penn State and Georgia sites thought groups of faculty, grad
students, student teachers. Communicate with each other throughout their
development. Convene a group of teachers to expand the set of vignettes. The
vignettes would be based on an event that actually happened for which the
teacher needed to draw on their mathematical knowledge instantaneously and
creatively. The writer should say what happened and describe the range of
possible mathematical responses. Enough would have to be included to allow the
reader to figure out the facilitative mathematical knowledge needed. The
members of the group to generate these vignettes would include secondary
mathematics teachers with a known ability to think creatively and well about
school mathematics.
Timeline: To
occur during Summer 2005. An early venue for feedback could be a session at the
Mid-Atlantic Center research conference. Later in the summer we could convene a
group of about 10 outstanding teacher-leaders who are especially suited for
this task. The goal would be to generate a total of 250 vignettes, 50 of which
would survive the final cut as we are developing the framework in step .
Activity: b. Have
the writing group and others expand on and generate rich sets of mathematical
responses for each of these vignettes. These sets of mathematical responses
would outline possible mathematical pathways that teachers could take in
response to the situation presented in the vignette and the mathematical
knowledge required of a teacher in order to pursue that path. They would probably include extensions,
connections, generalizations, and abstractions. They would be possibilities,
not to be considered an exhaustive set or a penultimate one.
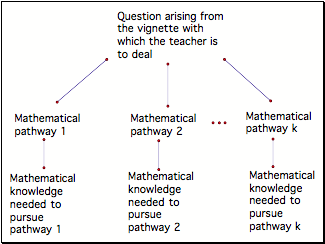
Timeline: To
occur during Summer 2005, some of it simultaneously with step a .
3.
Activity: Analyze
the vignettes and responses with respect to the big ideas that teachers would
need. This analysis might be done with research groups at Penn State and U of
Georgia working separately and then together in weekly(?) Polycom sessions.
Timeline: To
occur during Fall 2005. We could simultaneously get some reaction from “friends”
who would be willing to tell us things like which 5 out of 20 vignettes are the
best.
4.
Activity: a. This
analysis would be formed into a draft framework and a document about the work
of establishing the framework. The framework could serve two purposes: they
could provide guidance in doing practice-based innovative professional
development , they could help guide the field in thinking about research on the
mathematical knowledge of secondary teachers, they could help inform the
development of mathematics teacher educators, and they could inform mathematics
department about mathematics goals for secondary teachers . The framework could
also reveal the types of mathematical knowledge (e.g., representations) that is
needed frequently by teachers.
Timeline: To
occur during early Spring 2005.
Activity: b. As
framework is being constructed, create test items to illustrate the framework.
These would be intended as prototypical instruments. They could be in the form
of polished vignette to which teachers would need to respond.
Timeline: To
occur during early Spring 2005.
5.
Activity: Commission
experts in different areas to conduct reviews of the framework and vignette
packets. Each of these experts would be given a particular question about the
framework to address. They would be paid to produce papers that would be used
in the conference in step 6.
Timeline: To
occur during late Spring 2006 to early summer.
6.
Activity: A
conference would be held to provide feedback from the field on the framework
and on the items created to illustrate the framework. Feedback would be used to
modify the framework and the items. A range of people would be invited to the
conference. Mathematicians could help identify big ideas that were missing.
Experienced teachers would generate instances that might not fit the framework.
Curriculum developers could identify big curriculum ideas that were missing.
Researchers who have studied secondary mathematics could provide feedback on
the viability of the framework for providing a direction for research in the
area. Some of these individuals would be commissioned to write reviews prior to
the conference. The attendees
could also indicate which of the vignettes were most helpful in characterizing
the mathematical knowledge of secondary teachers.
Timeline: To
occur during late Summer 2006.
7.
Activity: Subsequent
work would test the framework in observational settings [Is this the best way
of testing the framework?]. Once it was felt that the framework adequately
captured the mathematical knowledge that secondary teachers need, assessment
instruments could be developed to use in research.
Timeline: To
be determined .
8.
Activity: A
product would be a small book with the framework and the illustrative items. Timeline: To be
determined .
9.
Activity: Connect
with MAA and NCTM to explore ways to use the framework in professional
development and in the work of mathematics departments.
Timeline: To be
determined .
Return