Situation
30: Translation of Functions
Prepared at University of
Georgia
Center for Proficiency in
Teaching Mathematics
6/30/05 – Bob Allen
10/6/05 – edited by Bob
Allen
Prompt
During a unit on functions, the transformation of functions
from their parent function is discussed in a class. For example, if the parent function is 
, then the child function 
would have a vertical translation of 4 units. When the class encounters the function 
, one student notes that the vertical translation of +3
Òmakes sense,Ó but the horizontal translation to the right of 2 does not Òmake
senseÓ with a – 2 within the function. As a teacher, how would you explain this?
Commentary
Note: Foci 1 and 2 use a parabola as a parent function only for demonstration purposes. One may substitute any function for the parabola.
Mathematical Foci
Mathematical Focus 1: Graphical Representation
One way to investigate this problem is to examine graphs of
parent functions and their respective children. Included are four QuickTime movies of 
undergoing
different translations, both vertically and horizontally. Looking at the various movies, students
can predict the general form of a parabola 
, where h and k predict the proper translation.
Mathematical Focus 2: Numerical Representation
Another way to explore horizontal translations is with a
numerical representation. With the
parent function as 
again, students
can investigate what happens with the values. ItÕs obvious to see that the values of the child function 
have shifted
right when compared to the parent function.
|
|
Parent |
Child |
Child |
|
x |
x^2 |
(x-1)^2 |
(x-2)^2 |
|
-5 |
25 |
36 |
49 |
|
-4 |
16 |
25 |
36 |
|
-3 |
9 |
16 |
25 |
|
-2 |
4 |
9 |
16 |
|
-1 |
1 |
4 |
9 |
|
0 |
0 |
1 |
4 |
|
1 |
1 |
0 |
1 |
|
2 |
4 |
1 |
0 |
|
3 |
9 |
4 |
1 |
|
4 |
16 |
9 |
4 |
|
5 |
25 |
16 |
9 |
|
|
|
|
|
|
|
|
|
|
|
x |
x^2 |
(x+1)^2 |
(x+2)^2 |
|
-5 |
25 |
16 |
9 |
|
-4 |
16 |
9 |
4 |
|
-3 |
9 |
4 |
1 |
|
-2 |
4 |
1 |
0 |
|
-1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
4 |
|
1 |
1 |
4 |
9 |
|
2 |
4 |
9 |
16 |
|
3 |
9 |
16 |
25 |
|
4 |
16 |
25 |
36 |
|
5 |
25 |
36 |
49 |
Mathematical Focus 3: Transformation of coordinate axes
This is from Smail, L. L.
(1953). Analytic Geometry and
Calculus. Appleton-Century-Crofts,
New York.
Let OX and OY be the original axes and let OÕXÕ and OÕYÕ
be a new set of axes, having a new origin OÕ and parallel to the old axes and having the same
senses.
Let the coordinates of the new origin with respect to the
old axes be (h, k). Let P be any point whose coordinates are (x, y)
referred to the old axes and (xÕ,
yÕ) when referred to the new
axes. Then 
Hence, if a translation of axes is made to a new origin OÕ whose coordinates with respect to the old axes are
(h, k), the relation between the old and new coordinates of any point is given
by 
and 
.
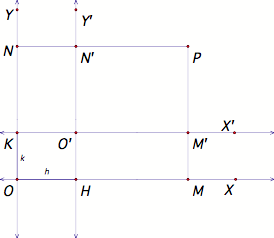Another
way to think about this is that the function is not the object that gets
translated. If the axes are
translated right and up, this means the function looks like it is translated to
the left and down. If the parent
function 
goes through a
translation of axes, then the new child function is 
which leads to 
.