Prepared at UGA
Center for Proficiency in Teaching Mathematics
9/29/05; revised
11/8/05—Amy Hackenberg
Prompt
A mathematics teacher, Mr. Fernandez,
is bothered by his ninth grade algebra students’ responses to a recent quiz on
radicals—simplifying fractions with radicals in the denominator, adding
radicals, and multiplying radicals. Some of them got mostly right answers but
many students added root 2 and root 3 and got root 5, and others simplified the
reciprocal of root 3 to root 3 divided by 9. Mr. Fernandez is disturbed over
the incorrect answers but even more disturbing to him is the sense that none of
this work is meaningful for his students—even for the ones who know the
rules.
What mathematical knowledge does Mr.
Fernandez need so that he might change his approach to radicals with his
students?
Commentary
The reason for Focus 1—roots of whole numbers—in
response to this prompt is primarily because this approach offers students the
possibility of building up their knowledge of radicals as lengths (of sides of
squares) so as to consider what is possible and not possible in combining and
operating with these relatively “new” (for ninth graders) mathematical objects.
By itself a focus on roots of whole numbers is insufficient to address all of the issues in the situation. Focus 2 brings in the issue of fractions that include radicals in the denominator.
Focus 3 and Focus 4 are included because
generating the notion of radicals as mathematical objects in relation to other
more familiar mathematical objects like whole numbers and fractions, is crucial
to constructing radicals as numbers, let alone combining and operating with
them. Part of the reason, I believe, that students will add
and get
![]()
has to do with their familiarity with whole numbers as mathematical objects and their familiarity with combining and operating with whole numbers. So I believe a major issue to address in this vignette is why those intuitions (built up over years!) do not hold. Note that students hardly have the same amount of time to build up intuitions about combining and operating with radicals. So Focus 3 and Focus 4 continue the development of this quantitative approach toward that end.
Mathematical
Foci[1]
Mathematical Focus 1—roots of whole
numbers
Mr. Fernandez can approach work on radicals by using a quantitative approach. That is, he can focus primarily on radicals as lengths, and then activity with radicals becomes geometrical problem solving at first, with only some numeric or algebraic calculation. Use of a tool like Geometer’s Sketchpad (Jackiw, 2001) will be helpful in this regard, although some of what’s mentioned below can occur without GSP.
Here’s the first question the teacher can pose to students: Starting with a square of area 1 square unit (see Figure 1), can you make a square of area 2 square units?

Figure 1
This problem can be solved in multiple ways, see Figure 2 below.
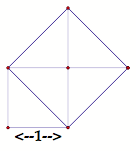
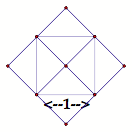
Figure 2
If a square with area 1 square unit has side root 1, which is 1, then a square with area 2 has side root 2. Some investigation here could occur with whether or not root 2 is “like the kind of numbers that we know about,” i.e., whole numbers or fractions. (Most students will agree it cannot be a whole number because they can’t think of a whole number that, when multiplied by itself, is 2. Fractions are another story but can be approached as noted in Focus 3).
Can students make squares of other areas using some of the techniques they have tried so far in making the square of area 2 (e.g., drawing diagonals and using the isosceles right triangles that are formed, circumscribing squares, etc.)? If the circumscribed technique (right side of Figure 2) is continued, squares with areas 4, 8, 16, etc., can be made, and so lengths that are root 4 (a whole number), root 8 (not a whole number), root 16, etc., can also be made. Note that all of this work can also be confirmed by the Pythagorean Theorem, examining the largest isosceles triangles formed at each iteration.
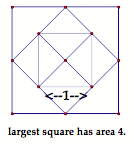
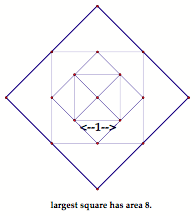
Figure 3
Next major question the teacher can pose to students: What about a square of area 3? How can this square be made? See Figure 4 below and page 1 of the GSP sketch VIG C 092905 radicals.gsp).
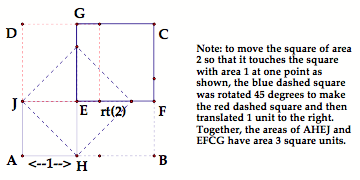
Figure 4
This sketch shows one way to “combine” a square of area 1 (AHEJ) and a square of area 2 (EFCG). The teacher can ask students to determine how they can use the diagram to produce a square of area 3. Note that using this diagram to make a square of area 3 is an example of the Pythagorean Theorem.
The biggest square, ABCD, consists of an area of 1 square unit, an area of 2 square units, and two rectangles that are each 1 unit by root 2 units. When the areas of the two rectangles are cut apart into 4 right triangular areas (with legs 1 and root 2 units) and separated, the remaining area in ABCD should also have area 1 + 2 = 3 (see Figure 5).
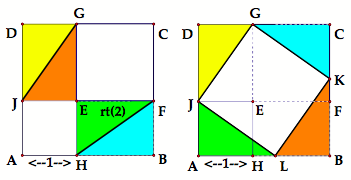
Figure 5
It remains to justify that this remaining area (GKLJ in Figure 5) is a square, which can be done using the 4 congruent right triangles (i.e., GKLJ is at least a rhombus and then it must have at least one right angle because, for example, angles AJL and DJG are complementary). So the sides of square GKLJ can be said to be
![]()
Then the teacher can ask students to use what they know to make a square with area 5, then a square with areas 6, 7, and beyond. Note that here the Pythagorean Theorem is used directly as a theorem about areas to make these area relationships and resulting lengths of
![]() ,
, ![]() ,
, ![]() , etc.
, etc.
Students can be challenged to locate all of these lengths on a number line in order to “fill in” the number line and to develop a sense of the relationship of these radicals to numbers like the whole numbers and fractions, which they already know something about (see pages 2, 3, and 4 of the GSP sketch VIG C 092905 radicals.gsp).
Mathematical Focus 2—roots of
fractions
The iterative approach to generating squares with areas that are powers of 2, described in Mathematical Focus 1, can go in the “other direction” to generate squares with areas that are fractions (i.e., starting with negative powers of 2). This exploration can lead to students developing radicals of some fractions (i.e., roots of negative powers of 2, such as
etc., some of which will be rational numbers and some of which will not). Note that once students have generated a length that is
they can make whole number multiples of it, such as
![]()
or fractional parts of it, such as
![]()
This activity is not sufficient for generating roots of any fraction or for considering why
![]()
but it is a start toward constructing roots of fractions as mathematical objects.
The question of how to construct
is not trivial! One possibility is to take a square of area 3 and subdivide it horizontally and vertically into thirds, thereby creating 9 squares, each with area 1/3. The length of the side of each these squares must be
![]()
and it is also
![]()
(thereby showing that the two must be equal). A similar approach can be taken to generate roots of other unit fractions.
Then, combinations of methods already described can be used to generate roots of non-unit fractions. For example, how can the square root of 2/3
![]()
be generated? One way is to use the circumscribing method on the square with area 1/3 to create a square with area 2/3.
Mathematical Focus 3—is root 2 a
fraction?
Although teachers may know a formal proof to show that this is not the case, the reasoning behind the proof—and ways to bring that reasoning out of students’ thinking—is a different kind of mathematical knowledge than just knowing a formal proof (I’ll argue).
One way to approach this question with students is to assume that
![]()
is a fraction, which can be written in lowest terms as a/b (a, b are non-zero whole numbers). If this is the case, then 2 = a2/b2, and 2b2 = a2. So this implies that a2 is even and so a is even (students will have to justify why!). But that means that there will be two factors of 2 in a2, so there must be two factors of 2 in 2b2. That means that b2 has to have one factor of 2 (can it?). Since if b2 has a factor of 2, it must have two factors of 2, and so b must have a factor of 2, then a and b both are even—but we assumed that the fraction a/b was written in lowest terms! So root 2 must not be able to be written as a fraction we know about, a/b in lowest terms where a and b are both non-zero whole numbers.
Mathematical Focus 4—addition and
multiplication of radicals
One of the underlying issues in the situation is why intuitions about addition, based on addition of whole numbers, do not hold with fractions or radicals, while intuitions about multiplication (again based on multiplication of whole numbers) do. (Note that one reason for this issue is that students assume that “square rooting” distributes across addition, i.e., the erroneous concept that
![]()
Although this kind of conception can be refuted using counterexamples, I have not included that here because my intent in this discussion is to develop a quantitative approach toward this issue.) So a major reason for taking a quantitative approach to work with radicals as outlined above is to investigate this issue, as I briefly describe here.
After radicals have been constructed as the lengths of sides of squares, questions can arise about how to combine these lengths. Lengths can certainly be added by joining them contiguously, but, since root 2 and root 3 cannot be written as whole numbers or fractions, we have no way to know whether we can notate their combination with a single graphic item, the way we can combine 2.5 and 3.75 into 6.25. So (at least for the moment),
![]()
is exactly that,
![]()
Furthermore, using lengths it is possible to develop intuitions about
![]()
NOT being equal to
![]()
(see page 5 of VIG C 092905 radicals.gsp). However, we can combine multiple lengths of
![]()
by determining how many of these we have, for example
![]()
Multiplication of two radicals like
![]()
can be thought about using similar triangles (see page 6 of VIG C 092905 radicals.gsp). Work with commutativity and associativity can occur by thinking about finding volumes of rectangular prisms that have radicals as lengths of sides (see page 7 of VIG C 092905 radicals.gsp). Working with commutativity and associativity is important so that students may be able to have a way to think about whether, for example,
![]()
is the same as
![]()
References
Jackiw, N. (2001). The Geometer’s Sketchpad (Version 4.4) [Computer software]. Emeryville, CA: Key Curriculum Press.