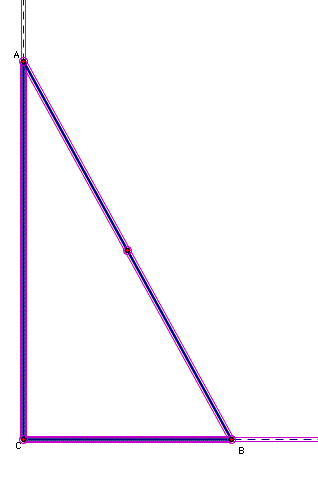
This is a geometry class. The physical situation of a ladder against the wall assumes that the ladder forms the hypotenuse of a right triangle and the legs of the right triangle lie along the wall and the ground at right angles:

We have a question about the midpoint of the hypotenuse of a right triangle. It is a rather early theorem in Geometry:

THEOREM: The midpoint of the hypotenuse of a right triangle is equidistant from the three vertices of the triangle.

 

There are multiple elementary proofs of this theorem. However, the theorem would lead quickly to the following picture:

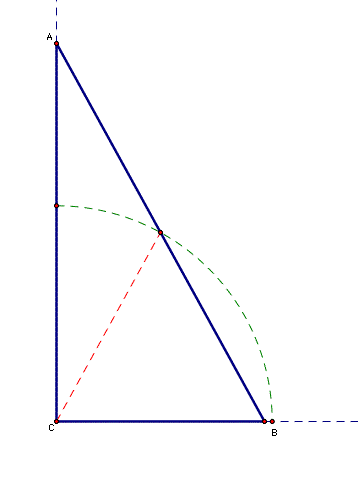
That is, as the ladder moves, the legs of the right triangle change but the hypotenuse (the ladder) remains the same length and the distance of its midpoint from the center will stay the same. The locus of the midpoint then lies along the arc of a circle with radius determined by the distance of the midpoint of the hypotenuse from the right angle vertex.

In any approach to this problem, it is important to reinforce the idea that this is an arc of a circle. In fact, the students should conclude that the arc is a quarter circle.

If the problem is modified slightly to allow the fixed point on the ladder to be someplace other than the midpoint, the locus of the point will be an arc of one-quarter of an ellipse. The ideas in Mathematical Foci 1-3 would be applicable to explorations where student could observe and conclude this locus. Of course, the locus for the midpoint is an arc of a 'degenerate' ellipse -- the arc of a circle.

Mathematical Focus 7

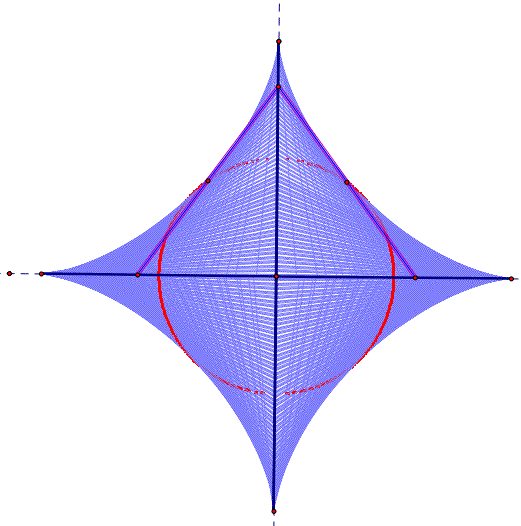
Generalizations. If we use GSP animations we can easily show the locus of the midpoints as a line segment is moved so its two end points move one end along the y-axis and one end along the x-axis.

The locus of the midpoints. Click here for a GSP animation.

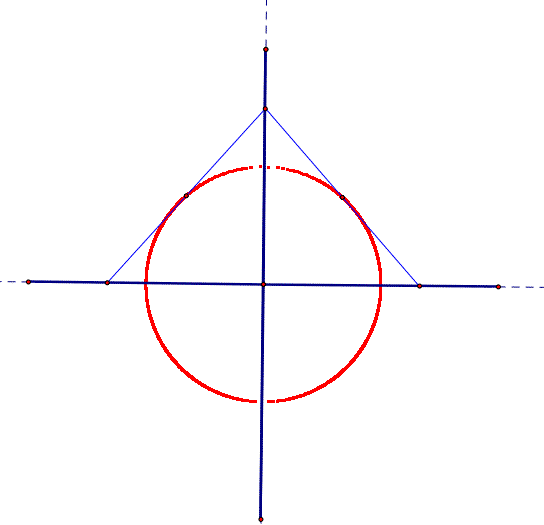
The locus on non-midpoints. Click here for a GSP animation.

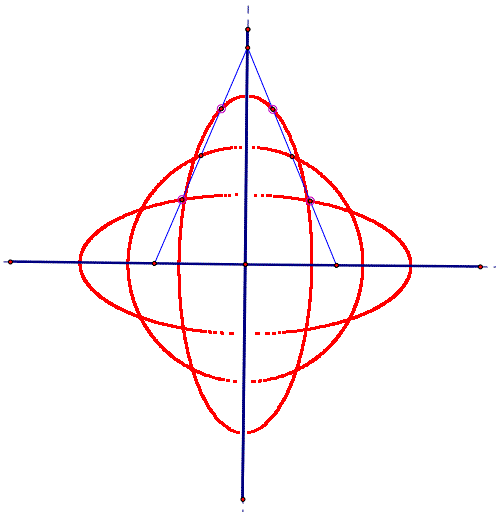
The locus of segment, Click here for a GSP animation.