Department of Mathematics Education

Some Explorations with Lemniscates.

by

Jim Wilson

1. Lemniscate of Bernoulli

Explorations:

B. Try

for different values of A, A > 0, Include A> 1, A< 1. Note there is no graph when A < 0. Why?

C. Try

for different values of B. Include B > 1, B <1.

What happens if B = 0? if B < 0? Try them!!

D. The geometric definition of the Lemniscate of Bernoulli is the locus of points with the product of the distances from two fixed points (foci) set at a particular constant. Construct such a locus with GSP.

E. Try in polar coordinates. (Note: It will work with Algebra Xpresser).

F. Try

G. Try

H. Try

I. Replace x by (x-1), y by 3y in G.

J. Replace x by sin(x) and y by sin(y) in G. Replace the coefficient 50 by smaller numbers, such as 2, 3, 4 or -1, -2, -3.

2. Lemniscate of Gerone

Explorations

B. Compare the Lemniscate of Bernoulli and the Lemniscate of Gerone.

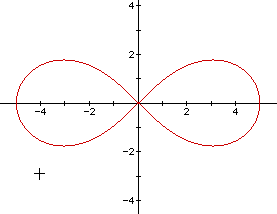
C. Write an equation for this graph:

D. Write an equation for this graph:

E. Is there a geometric construction, as a locus, for the Lemniscate of Gerone? If so, implement it on GSP.