
Department of Mathematics and Science Education

The Nine Point Circle is seldom included in school mathematics, yet it is a topic that can easily be understood and explored with some basic and elementary background in geometry. The goal in this presentation is to show some points that open the way for exploration.
Usually, if the Nine Point Circle is presented in school mathematics it is as an interesting sidelight or theorem without much insight into its relationship to the geometry of triangles. That is, one may find a statement like:
For any triangle ABC, there is a circle that contains the feet of the perpendiculars from the vertices, the midpoints of the sides, and the midpoints of the segments from the vertices to the orthocenter.
Sometimes with "Prove that . . ." The usual student (and teacher response) is "Who cares?" That is unfortunate because this topic as an interesting and rich history and substance.
I think it is useful to first consider some concepts associated with triangles. It used to be a part of the geometry curriculum to prove the concurrency of the three medians (the centroid), the concurrency of the perpendiculars from the vertices to the opposite sides (the orthocenter), the concurrency of the perpendicular bisectors of the sides of the triangle, and the concurrency of the bisectors of the interior angles (incenter) or the concurrency of the bisectors of each interior angle and two opposite exterior angles (excenters). These are stated without proof here. Proofs of these concurrencies are worthwhile problems (See JWilson EMAT 6600 Mathematical Problem Solving).
Click HERE for a Demostration Triangle in GSP to follow along with explorations
1. The CENTROID (G) of a triangle is the point of currency of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.
Each of the medians divides the triangular region into two equal areas. The centroid (usually represented by G) is often referred to as the 'center of mass' of the triangle. There are several interesting and important theorems regarding the centroid and the medians. For example. the centroid divides each median in a ratio of 2:1. That is on any median, the distance of the centroid from a vertex is twice the distance to the midpoint of the opposite side. Also, the three medians through the centroid divides the area of the triangle into six smaller triangles of equal area.
We can use GSP to construct the centroid and explore its location for various shapes of triangles.
2. The ORTHOCENTER (H) of a triangle is the point of concurrency of the three lines containing the altitudes.An altitude is a perpendicular segment from a vertex to the line of the opposite side. (Note: the foot of the perpendicular may be on the extension of the side of the triangle.) It should be clear that H does not have to be on the segments that are the altitudes. Rather, H lies on the lines extended along the altitudes.
We use GSP to construct an orthocenter H and explore its location for various shapes of triangles, including obtuse triangles.
If one side of the triangle is fixed and the other vertex moved along a line parallel to the fixed base, the locus of the ortocenter is the parabola. If the line is not parallel to the base, the locus is the hyperbola.
3. The CIRCUMCENTER (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle.Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle. Note: C may be outside of the triangle. Thus the circumcenter is the point of concurrency of the three bisectors of the sides of the triangle.
We can use GSP to construct the circumcenter C and explore its location for various shapes of triangles. It is the center of the CIRCUMCIRCLE (the circumscribed circle) of the triangle.
Geometer's sketchpad also lets us see a dynamic construction of the circumcircle. First, we use a small radius to contruct congruent circles at each vertex.
Then we allow the radius to increase in length.
When the circles overlap, the intersections trace out the perpendicular of the respective side,.
When the radius is more than half the longest side of the triangle, then all three perpendicular bisectors are shown with the point of concurrency being the circumcenter. (This is NOT a proof; it is only a demonstration). The concept here is that points on the perpendicular bisectors are equidistant from the endpoints of side.
4. The INCENTER (I) of a triangle is the point on the interior of the triangle that is equidistant from the three sides.Since a point interior to an angle that is equidistant from the two sides of the angle lies on the angle bisector, then I must be on the angle bisector of each angle of the triangle, i.e. it is the point of concurrency.
We use GSP to show a construction of the incenter I and explore its location for various shapes of triangles. The incenter is the center of the INCIRCLE (the inscribed circle) of the triangle.
5. The Euler line (or more properly, the Euler segment). If in the same triangle we construct H, G, and C, we can see with exploration, pose for proof, the following:
The orthocenter, centroid, and circumcenter are colinear.
The centroid is two thirds the distance from the orthocenter to the circumcenter.
The incenter is not on the Euler line except when the triangle is isosceles.
6. Take any triangle. Construct a triangle connecting the three midpoints of the sides. This is called the MEDIAL triangle.It is similar to the original triangle and one-fourth of its area.
Compare the Euler segments for the original triangle and the medial triangle. In the figure at the right, the Euler segment for the medial triangle is given in a heavier line segment.
The Euler segment appears to be half the length of the Euler segment in the original triangle, has the same centroid, and the circumcenter of the original triangle is the orthocenter of the medial triangle (all of these are nice problems for proof).
7. Constuct the perpendiculars from each vertex of a given triangle and construct a new triangle connecting the feet of the altitudes. This is called the ORTHIC triangle.
We can compare the Euler segment for the original triangle and the orthic triangle:
One problem for a proof is that the circumcenter of the orthic triangle is at the midpoint of the Euler segment for the original triangle.
8. Take a triangle and locate its orthocenter. Now do a dilation of one-half using the orthocenter as the center of dilation. The images of the three vertices are shown
Construct the triangle with the three image points as the vertices. These image points are the midpoints of segments from the vertices to the orthocenter and the resulting triangle is a dilation of the original triangle by one-half with the orthocenter as the center of dilation.
The two triangles have the same orthocenter.
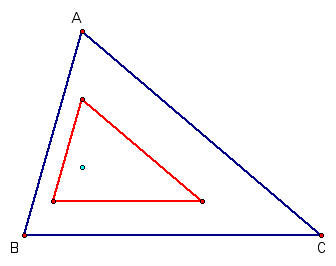
Compare the Euler segments of the original triangle and this image triangle.
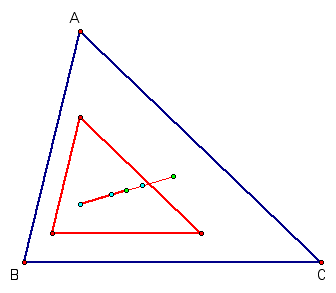
Conjecture to be proved: The Euler segment of the image triangle lies along one half of the Euler segment for the original triangle and the circumcenter is at the midpoint.
The Nine Point Circle Now, let's put it all together. First, lets look at the medial triangle, orthic triangle, and the image triangle in the same construction:
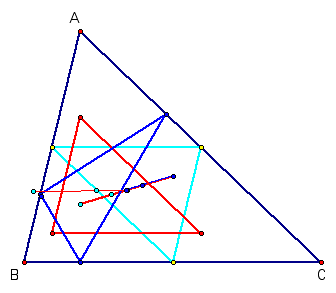
These three special sub-triangles ALL HAVE THE SAME CIRCUMCENTER. Therefore there is a circle that is the common circumcircle for these three special sub-triangles. That is the nine point circle.
In Europe the nine point circle is often referred to as the Euler circle. In some writing it is called the Feuerbach circle. In 1765 Euler proved that the circle through the three feet of the altitudes also passed through the midpoints of the sides. Sometime later, Feuerbach showed that the three midpoints of the segments from the vertices to the orthocenter were on the same circle. Someone else, much later, coined the term 'nine point circle.'
Lets return to the image triangle formed by a dilation of the original triangle and add the circumcircle and circumcenter of the orgininal triangle to the construction:
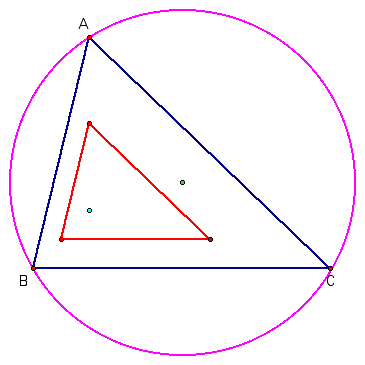
Now a dilation of the circumcircle and circumcenter will produce a circle that is the circumcircle of the image triangle with center at the midpoint of the Euler segment of the original triangle.
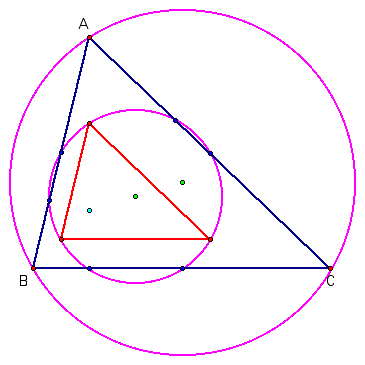
This new circle crosses each of the sides in two places, generally, and a proof would depend on showing that on each side, one of those two points is the foot of the perpendicular and the other is the midpoint of the side.
Some additional lines may be helpful. Let H be the orthocenter. Construct AT as a diameter of the circumcircle. Lines HC and TB are perpendicular to AB since CH is along an altitude of the triangle and ABT is a right triangle. Therefore HC is parallel to TB. Similarly, lines BH and TC are parallel because both are perpendicular to AC.
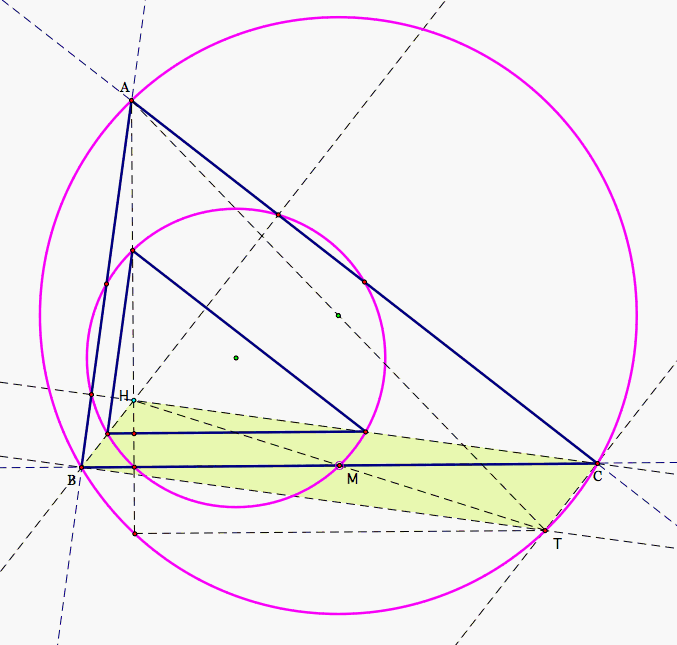
So, BHCT is a parallelogram. The diagonals HT and BC will bisect each other and therefore since HM is one half of HT, M is on the circle and the midpoint of BC. The midpoints on sides AB and AC could likewise be confirmed as lying on the dilation image. Click HERE for the GSP sketch.
The intersection of the image circle at the foot of the perpendicular can be established by showing triangles HCF and SCF are congruent.
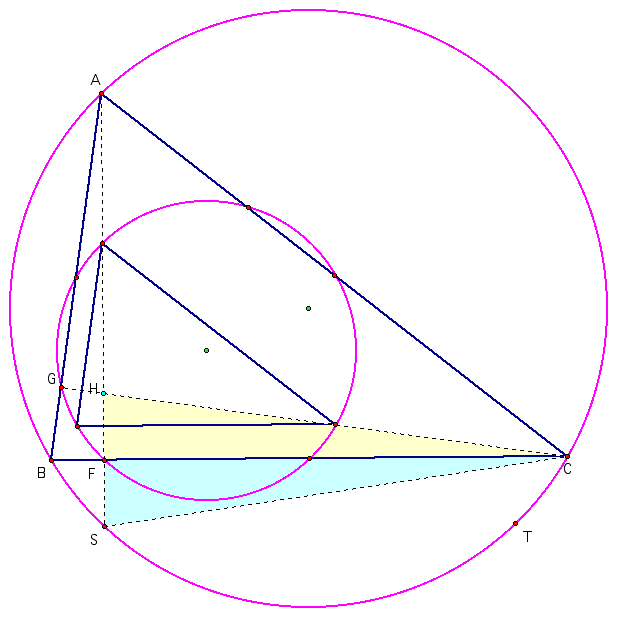
Angle BCG = 90 - m(angle B) from the right triangle CGB. However, this is also the measure of angle BAS from the right triangle AFB. Since both angles BAS and BCS subtend the same arc (BS) we have that angle SCF is congruent to angle BCF. Angles HFC and SFC are right angles and FC is a common side so we have the two triangles congruent. We conclude that the point F on the image circle is at the foot of the perpendicular. Similar arguments would hold for the feet of the perpendiculars on side AC and AB.
The feet of the perpendiculars are the intersection points by force of the dilation with the orthocenter as the center of dilation.
Likewise the center of the nine point circle, by force of the dilation, is one half the distance from the orthocenter to the circumcenter. That is, the center of the nine point circle is at the midpoint of the Euler segment.
The nine point circle has one-have the radius of the circumcircle and its center is mid-way from the orthocenter to the circumcenter.
Note, every line segment from the orthocenter to the circumcircle is bisected by the image circle (the nine-point circle).
Try this: The tangent lines to the nine point circle at the midpoints will form a triangle that is similar to the orthic triangle (with sides that are parallel). Click HERE for a GSP Sketch.
Consider the triangle, its INCIRCLE, and its three EXCIRCLES. Click HERE for a GSP Sketch.
When the nine point circle is constructed for the triangle formed by the three excenters, it is the circumcircle of the original triangle.
Further, when the nine point circle is constructed for the triangles formed by the incenter and two of the excenters, each of them has the circumcircle of the original triangle as its nine point circle.
Nine Point Conics.
Ceva's theorem considers an arbitrary point as the center and Cevians through that point from the vertex to the opposite side.
Begin with a triangle and select an arbitrary point P. Construct the Cevians through that point. Using P as the center of dilation, dilate the triangle and its vertices by one-half. The image triangle will be similar to the original triangle with parallel sides of half the length.
Construct a conic using any five of the six points: the three vertices of the image triangle and the three feet of the Cevians.
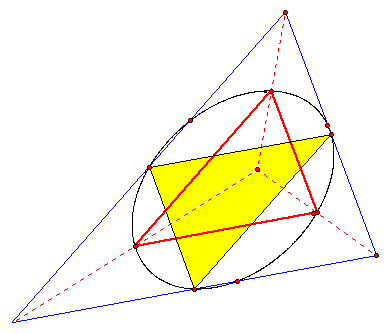
A conic is formed -- any five points determine a conic. It is to be proved that the midpoints of the triangle will be on the conic.
When P is inside the triangle, an ellipse is produced. In the six outside regions produced by extending the sides of the triangle, three of them lead to the conic being the hyperbola and the other three produce ellipses.
Click HERE for a GSP sketch.