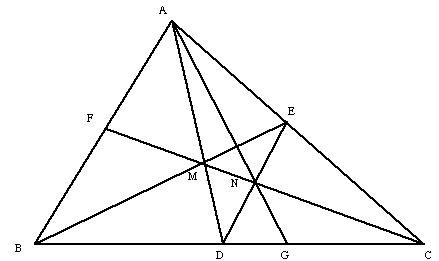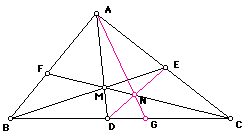
We show a construction and a general ratio result for triangles that can be used to segment a line into various parts. The construction has as a special case the GLaD construction. (Mathematics Teacher, January 1997).

Click here for a Geometer's Sketchpad file for this construction.

Applying Ceva's theorem to triangle ABC and the point M, we obtain:

Also, from Jim Wilson's result, we have:

Now, apply Ceva's theorem to triangle ADC and the point N. We have:

Substituting for AM/MD,

Simplifying,

From this:

Q.E.D.

If D is the midpoint of BC, that is, AD is a median, and M is any point on the median, then we have:

and, therefore,

In other words,

If we repeat the construction with N as the point, we can obtain the point H such that

and so on. Thus, we can segment the line BC into integral divisions without drawing any parallel lines. Just the location of the midpoint D of BC is required. (Picture)

Click here to see a Geometer's Sketchpad construction of these integral divisions.

If we extend the point B to infinity along CB, then the line ME will become parallel to BC. Also, if we extend the point A to infinity along BA, DM and GN, which are segments of DA and GA, will become parallel. Then, our construction begins to resemble a GLaD-like construction applied to the quadrilateral DMEC which has actually become a parallelogram (see also Jim Wilson's comments on the GLaD construction.)

In exploring the literally hundreds of various distances, ratios and areas that result in repeating this construction with the Geometer's Sketchpad, we found very interesting relationships. Perhaps some of these are worth exploring.