The SaRD Construction:
An Elegant Solution for Euclid's Partitioning Problem
By
SriRanga S. Dattatreya
(with help from Ravi E. Dattatreya)
December 14, 1996
Summit, New Jersey
Requirement.
Partition a line segment into a given number of equal parts.
Construction.
Let AB be the given line segment. Draw a line
segment AC such the AC is perpendicular to AB
at the point A. Draw a line L as shown, such
that L is perpendicular to AB at B. (Note: AC
and the line L do not have to be perpendicular to AB, as long as AB and
L are parallel.)
Now, mark a point D on L such that the length
of the segment BD is (n-1) times the length
of the segment AC. Also, ensure that D and C
lie on opposite sides of the line segment AB. Draw the segment
CD. The segments AB and CD intersect
at P.
AP is the required partition. Length AP = (1/n)
length AB.

Geometric Proof:
See Figure 1. Triangles CAP and DBP
are similar, because:
Angle A = angle B = 90 by construction
Angle APC = angleBPD, vertically opposite angles
The ratio CA:BD is equal to the ratio AP:PB,
by similarity of the triangles.
Ratio CA:BD is equal to 1:(n-1) (by construction).
Thus, AP:PB is equal to 1:(n-1) (from result
above).
Or, AP:AB is 1:n. (middle school algebra)
Q.E.D.
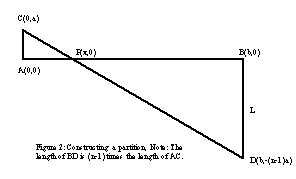
Algebraic Proof:
See figure 2. Let the point A be the origin, (0,0).
Let the length AB be equal to b, so that point
B is at (b,0). Let the lenght AC
be a, so that the point C is at (0,a)
and the point D is at (b, -(n-1)a), by construction.
The line CD meets the x-axis at P.
X-intercept is AP. The line CD
meets the y-axis at C. Y-intercept
is AC.
The slope of the line CD is [a - (-(n-1)a)] / [0 - b],
using basic principles. This simplifies to -(na/b). The y-intercept
of this line is a, at C. Thus, the equation
of this line is y = (na/b) x + a, in the standard y
= mx + c format. To get the x-intercept,
set y to zero to get, x = -a / (na/b) = - ab/na = -b/n.
That is, the distance AP is b/n. Since
the distance AB is b, the point P
represents the required nth partion.
Q.E.D.
Why do we prefer SaRD Construction to the GLaD Construction?
SaRD is much more simple to construct geometrically.
SaRD gives the student insight as to why it works.
SaRD is not an iterative procedure, unlike GLaD.
SaRD reminds one of Euclid's own construction.
SaRD can handle non-integral partitions, e.g., 1/(2.5),
as long as we can mark off the appropriate length BD to be 1.5
times the length AC.
SaRD can also handle multiples. For example, to find a point E
on the line AB (extended) such that AE is n-times
the length AB, then, choose the point D to be
on the same side as C, and make BD equal to
(1-(1/n)) of AC.
E-Mail


