1. Solve (or explain why it is impossible to solve)
1. 4 : 0.25
2. 0.2 : 0.8
3. 0.8 : 0.2
4. 0.25 : 0.6
5. 8.25 : 4.5
6. 3![]() x 5
x 5
7. ![]()
8. ![]() : 4
: 4
2. A student used the following procedure to multiply 0.25 x 5.25
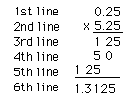
Do you think that the student's answer is correct? Yes/No.
Explain why lines 4, 5, and 6 were written in the way they were?
Explain the position of the decimal point in line 6.
3. A student solves the expression 5 : 0.8 in the following manner:
1st step ![]()
2nd step ![]()
3rd step ![]()
Explain steps 1 and 2.
What is the answer to the original division problem (5 : 0.8)?
4. A student used the following procedure to solve ![]() : 3.
: 3.
Stage 1 ![]()
Stage 2 ![]()
Stage 3 ![]()
Stage 4 ![]()
Do you think that the student's answer is correct? Yes/No
Explain Stages 1 and 2.
5. A student used the following procedure to compare the fractions ![]() .
.
He wrote : 14 x 13 < 11 x 17
Hence ![]()
Do you think that the student's answer is correct? Yes/No
Do you think that the method he uses for comparing fractions is adequate? Yes/No
Explain your answer.
6. In the division problem a : b = c, a is the dividend, b is the divisor and c is the quotient.
In the multiplication problem a x b = c, a and b are factors and c is the product.
Circle the correct answer and explain your choice:
In a division problem, the dividend can be smaller than 1.
Yes / No. Why?
In an addition problem, the sum can be smaller than one of the addends.
Yes / No. Why?
In a multiplication problem, the product is always greater than 1.
Yes / No. Why?
In a multiplication problem, the product is always greater or equal to each factor.
Yes / No. Why?
In a division problem, the dividend must be greater than the divisor.
Yes / No. Why?
In a division problem, the dividend must be greater than the quotient.
Yes / No. Why?
In a division problem, the quotient must be a whole number.
Yes / No. Why?
In a division problem, the divisor must be a whole number.
Yes / No. Why?