

Very often in our mathematics classes we need to have examples of applications of the concepts and procedures we teach. Similar figures, intuitively and formally, are figures with the same shape but not necessarily the same size. Similarity concepts are studied as early as third grade and encountered throughout the curriculum.
In the September/October 1998 issue of Workbench, an article on "Felling a Tree Safely" included an inset describing a method used by a logging instructor to gauge the height of a tree and thereby determine where the top of the tree would fall when the tree is felled.
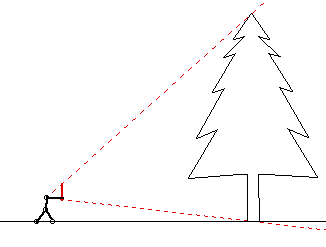
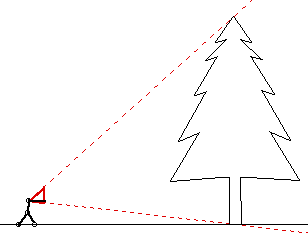
The method is described by marking a gauge stick the same length as your reach. When the gauge stick is held vertically in front of you at arms length, your eye and the two ends of the gauge stick create a triangle that has about the same base and height. By moving toward or away from the tree until you can sight the top of the tree over the upper end of the gauge stick and sight the cut line of the tree where you have marked your reach, then a similar triangle is formed for your eye, the top of the tree, and the cut line of the tree.
 .
. .
.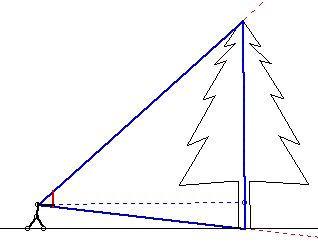
The inset indicates that a proportional triangle is obtained, a slight misnomer. Similar triangles are obtained. Similar triangles have corresponding sides in the same proportion and therefore the height of the tree and the distance you are standing from it are the same.
The arc in Box C of the inset should, as the text indicates, intersect the ground about where you are standing rather than just below your outstretched hand. The handle of an axe can be used to make the gauge stick.
The method works on level ground. How would it be modified if the tree was on a slope and you wanted to fell the tree downhill? uphill?
There is nice opportunity in this context to stress concepts of approximation and appropriate levels of precision.