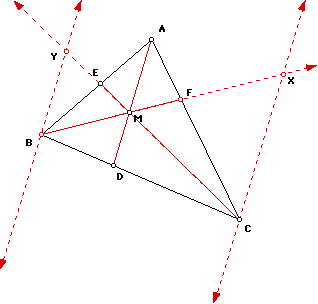
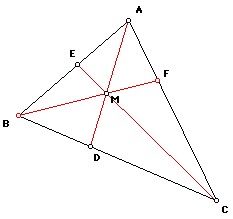
Given any triangle ABC with a point M in the interior. Segments
through M from each vertex to the opposite sides of the triangle
are Cevians and Ceva's theorem says that the product of
the ratios of the pairs of segments formed on each side of the
triangle by the intersection point is equal to 1, where the ratios
are taken in same orientation on each side. Further, if the ratio
formed by any three Cevians is equal to 1, then the three Cevians
are concurrent.
That is:
Who is Giovanni Ceva?
The usual proof of Ceva's Theorem involves consideration of
similar triangles in the augmented figure below.