Triangle Centers
by Kristina Dunbar, UGA
![]()
![]()
In this assignment, we will be investigating 4 different triangle centers: the centroid, circumcenter, orthocenter, and incenter.
The centroid of a triangle is constructed by taking any given triangle and connecting the midpoints of each leg of the triangle to the opposite vertex. The line segment created by connecting these points is called the median. You see the three medians as the dashed lines in the figure below.
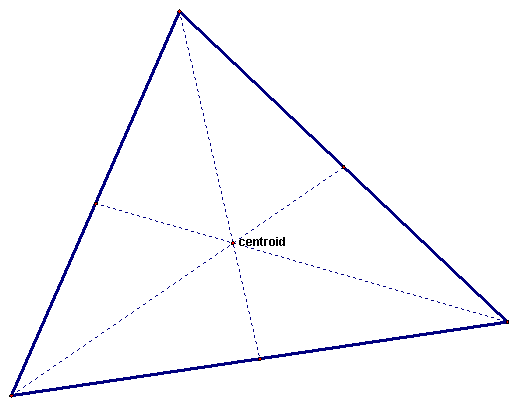
No matter what shape your triangle is, the centroid will always be inside the triangle. You can look at the above example of an acute triangle, or the below examples of an obtuse triangle and a right triangle to see that this is the case.
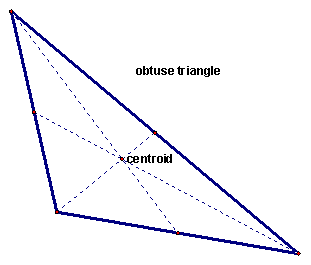
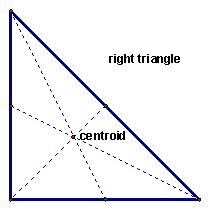
The centroid is the center of a triangle that can be thought of as the center of mass. It is the balancing point to use if you want to balance a triangle on the tip of a pencil, for example.
If you have Geometer's Sketchpad and would like to see the GSP construction of the centroid, click here to download it.
The circumcenter is the center of the circle such that all three vertices of the circle are the same distance away from the circumcenter. Thus, the circumcenter is the point that forms the origin of a circle in which all three vertices of the triangle lie on the circle. Thus, the radius of the circle is the distance between the circumcenter and any of the triangle's three vertices. It is found by finding the midpoint of each leg of the triangle and constructing a line perpendicular to that leg at its midpoint. Where all three lines intersect is the circumcenter.
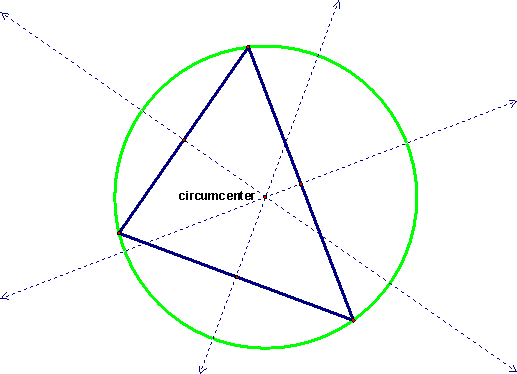
The circumcenter is not always inside the triangle. In fact, it can be outside the triangle, as in the case of an obtuse triangle, or it can fall at the midpoint of the hypotenuse of a right triangle. See the pictures below for examples of this.
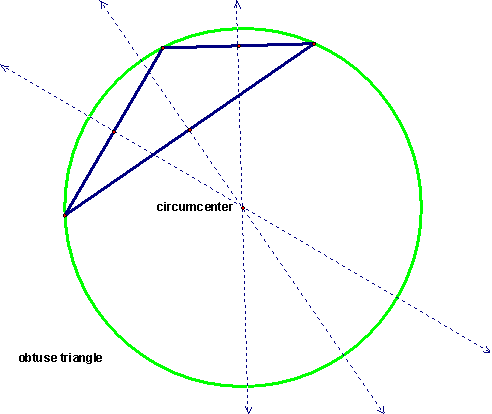
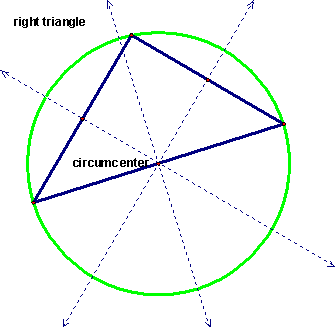
You see that even though the circumcenter is outside the triangle in the case of the obtuse triangle, it is still equidistant from all three vertices of the triangle.
If you have Geometer's Sketchpad and would like to see the GSP construction of the circumcenter, click here to download it.
The orthocenter is the center of the triangle created from finding the altitudes of each side. The altitude of a triangle is created by dropping a line from each vertex that is perpendicular to the opposite side. An altitude of the triangle is sometimes called the height. Remember, the altitudes of a triangle do not go through the midpoints of the legs unless you have a special triangle, like an equilateral triangle.
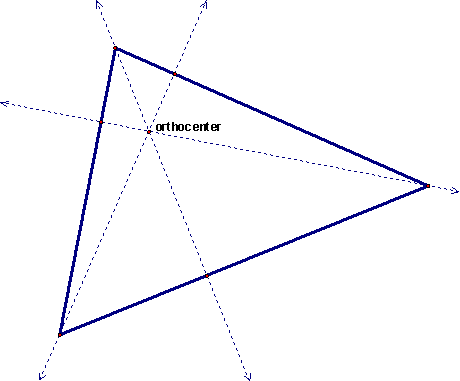
Like the circumcenter, the orthocenter does not have to be inside the triangle. Check out the cases of the obtuse and right triangles below. In the obtuse triangle, the orthocenter falls outside the triangle. In a right triangle, the orthocenter falls on a vertex of the triangle.
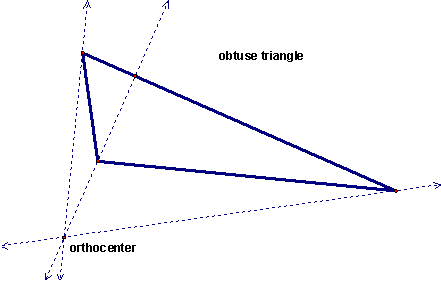
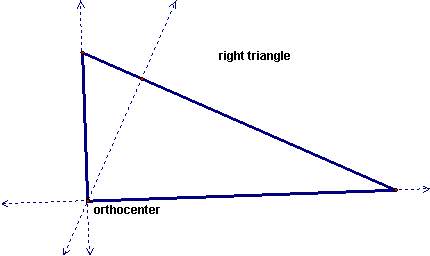
If you have Geometer's Sketchpad and would like to see the GSP construction of the orthocenter, click here to download it.
The incenter is the last triangle center we will be investigating. It is the point forming the origin of a circle inscribed inside the triangle. Like the centroid, the incenter is always inside the triangle. It is constructed by taking the intersection of the angle bisectors of the three vertices of the triangle. The radius of the circle is obtained by dropping a perpendicular from the incenter to any of the triangle legs. It is pictured below as the red dashed line.
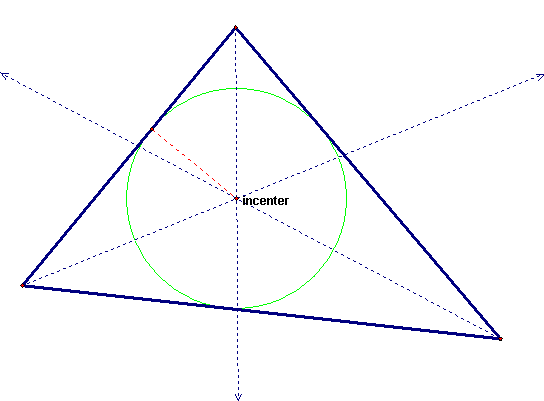
To see that the incenter is in fact always inside the triangle, let's take a look at an obtuse triangle and a right triangle.
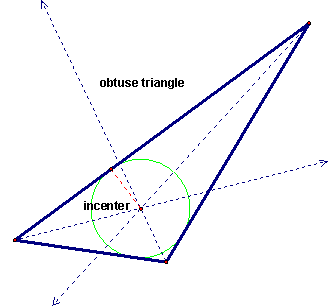
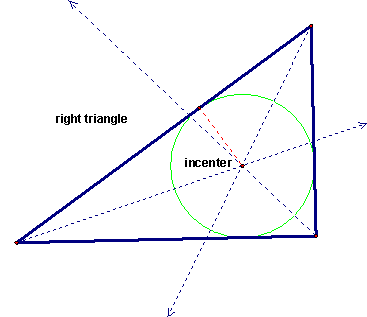
If you have Geometer's Sketchpad and would like to see the GSP construction of the incenter, click here to download it.
There is an interesting relationship between the centroid, orthocenter, and circumcenter of a triangle.
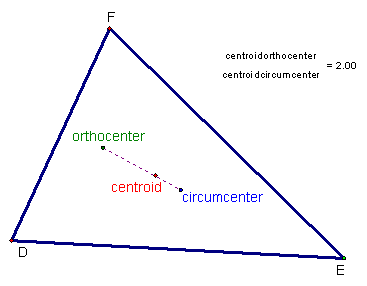
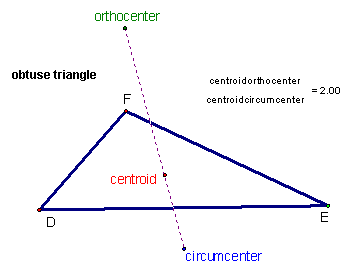
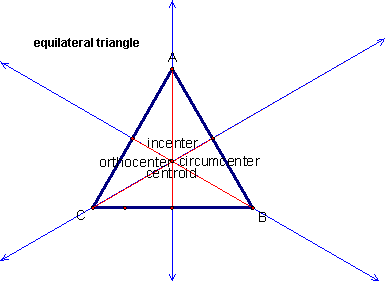
If you have Geometer's Sketchpad and would like to see the GSP constructions of all four centers, click here to download it. This file also has all the centers together in one picture, as well as the equilateral triangle. It can be used to generate all of the pictures above.
SKIP to Assignment 5: GSP Scripts.
![]()
![]()