

Day 3/Lesson 3: Similar Polygons
Goals:
1. Identify similar polygons
2. Use similar polygons to solve problems.
Opener: Explore the Polygons in GSP
Introduction:
Recall that two shapes are congruent if they have the same shape and size. When two shapes have the same shape but different sizes, we call the shapes similar. You can also think of similar objects or shapes as scaled versions of each other.
Example: Toys cars and airplanes that are scaled down versions of the real objects. In this section we will just concentrate on similar polygons.
Recall that a polygon is a closed shape consisting of a finite number of line segments that do not cross each other. Below are a few examples of polygons:

Definitions:
1. Polygons whose corresponding angles are congruent and whose corresponding sides are proportional are called similar polygons.
Example:
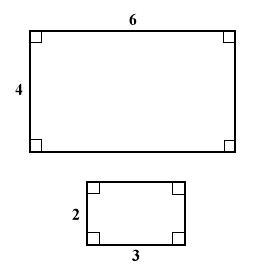
Check the angles and corresponding sides:
All the angles in a rectangle are congruent to each other and now check that the sides are proportional to each other.

2. Scale factor: If two polygons are similar, then the ratio of the lengths of the two corresponding sides is the scale factor.
The scale factor=k in the above example is determined the following way:
2*k=4, so k=2.
Now we will have the same relationship between the other two sides:
2*k=3, so k=2.
Solving
Problems with Similar Polygons:
There are three ways to solve for a missing side length of a polygon when you are given a pair of similar polygons.
1. "Scale Factor" Method: Given that two polygons are similar, there is a scale factor between the corresponding sides of the polygons, call the scale factor, k. We can use the relationship between two of the corresponding sides, to find the rest of the corresponding sides.
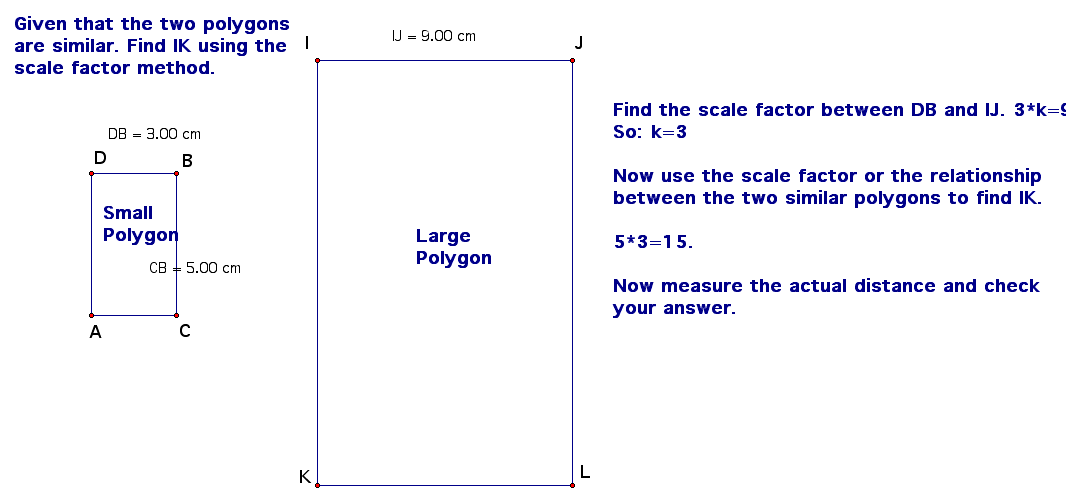
Click here to measure the side IK.
2. "Relative Size" Method: Now we will use the relationship between the sides of one polygon to find the lengths of the sides of the other polygons.

3. Set up a proportion to find the missing side length. We know that a proportion is two ratios that are equal to each other, so you can use either ratio, the relative size or the scale factor, and find the missing side.

Applications
Using Similar Polygons:
1. A large flag flown in front of a school is 4ft. tall by 8ft. and 5in. wide. Suppose you want to make a scaled down version of the flag. If you want the flag to be 2ft. tall, how wide should the scaled down version of the flag be? Use any of the three methods we have just discussed.
Hint: Make sure that all of your units are the same in the ratios that you set up.
Theorem:
If two polygons are similar, then the ratio of their perimeters is equal to the ratios of their corresponding side lengths.

Explore these similar polygons in GSP see if the theorem holds: