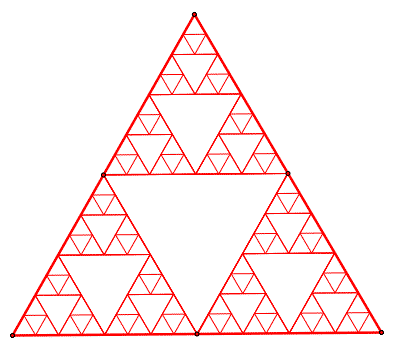
The Sierpinski triangle is a fractal described in 1915 by Waclaw Sierpinski. It is a self similar structure that occurs at different levels of iterations, or magnifications. We can use Geometer's Sketchpad to construct these types of triangles, and then compare them to the pattern of Pascal's Triangles.
Below, a pattern has begun by finding the midpoints of the line segments of the largest triangle. Then, by connecting these midpoints smaller triangles have been created. This pattern is then repeated for the smaller triangles, and essentially has infinitely many possible iterations. This is called Sierpinski's triangle.

The Sierpinski triangle generates the same pattern as mod 2 of Pascal's triangle. That is to say, the even numbers in Pascal's triangle correspond with the white space in Sierpinski's triangle. In fact, Pascal's triangle mod 2 can be viewed as a self similar structure of triangles within triangles, within triangles, etc.
See how this compares to Pascal's Triangle in mod 2!
View the GSP construction and tool for this figure, and adjust the number of iterations shown.
The triangle below was generated from iterations by trisecting the line segments that make up the largest triangle. Does this new iteration correlate to the pattern found in Pascal's triangle mod 3?
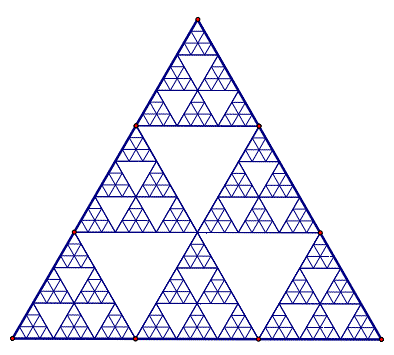
See how this compares to Pascal's Triangle in mod 3!
View the GSP construction
and tool for this figure, and adjust the number of iterations
shown.
This triangle began by dividing the line segments of the largest triangle into four equal parts. Then, once new triangles were drawn the pattern was repeated. While this does not correspond to Pascal's triangle mod 4, it is interesting to compare this triangle to the ones above!
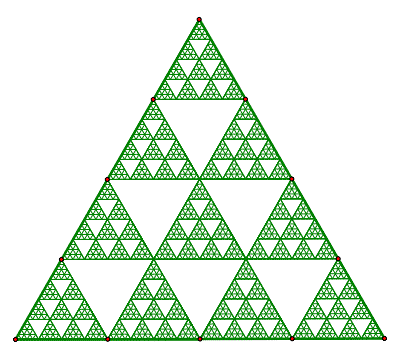
See how this does not correspond to Pascal's Triangle in mod 4!
View the GSP construction
and tool for this figure, and adjust the number of iterations
shown.
For more information on Sierpinski Triangle, visit these web sites
Return
to Essay 1: Pascal's Triangle and Modular Exploration