Assignment 4:
Circumcenter of a triangle
By Dorothy Evans
The CIRCUMCENTER of a triangle is the point in the plane
equidistant from the three vertices of the triangle. Since a point equidistant
from two points lies on the perpendicular bisector of the segment determined by
the two points, the circumcenter (labeled below) is the point of concurrency of
the three perpendicular bisectors of each side of the triangle.
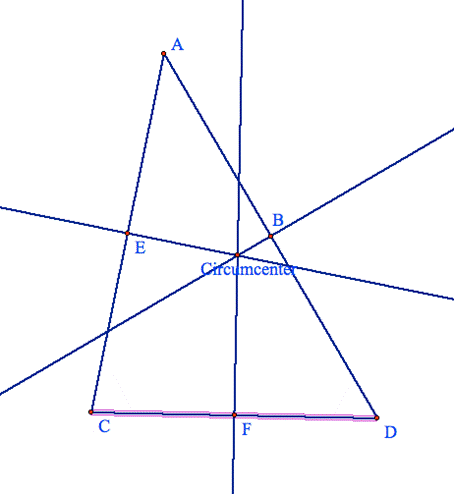
The basic construction of the circumcenter
is to identify the midpoints of the original triangle.† In the picture above the original triangle is
triangle DACD.
The circumcenter was constructed by identifying the midpoints of
the segments AC, CD, and DA.† Then a
perpendicular line was drawn through the midpoints perpendicular to the side
segment.
This particular example is of an acute scalene triangle.† Letís now explore what happens to the
circumcenter in other types of triangles.
First letís look at a right triangle.
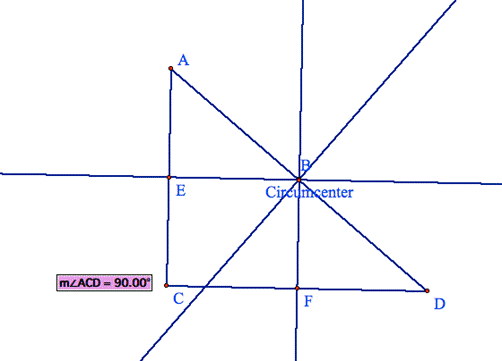
Notice
that the circumcenter is now on the segment AD
of the triangle ACD
I
wonder what would happen if the right triangle was an isosceles right triangle?
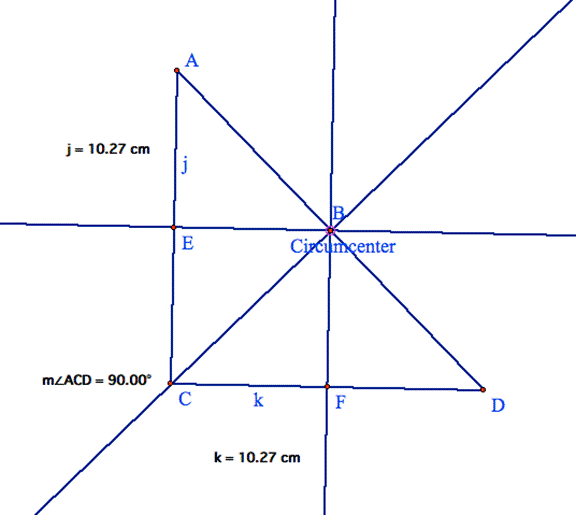
Notice
this time the line from the midpoint of AD perpendicular to AD now passes
through the vertex C of triangle ACD.
Now
that we have explored acute and right triangles letís now look at obtuse
triangles.
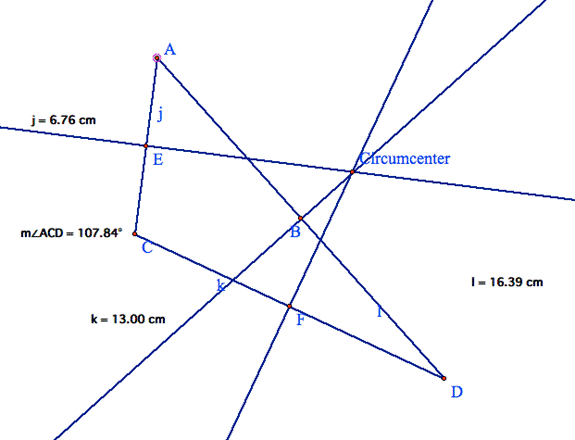
Wow
Ö What happened?
The
circumcenter is now outside of the triangle
ACD.
Hmmm,
what would happen if the obtuse triangle was isosceles?††

Now
how cool is that?
The
circumcenter of an obtuse isosceles triangle
is outside the triangle and the perpendicular bisector passes through the
obtuse angle of the triangle.
Letís
also note where the circumcenter gets its name.†
The circumcenter is also the center of circle that the triangle is
circumscribed inside of.† You may be
asking yourself, ďWhat does circumscribed mean?Ē† Letís look at the picture of our triangle and
itís circumcircle.†
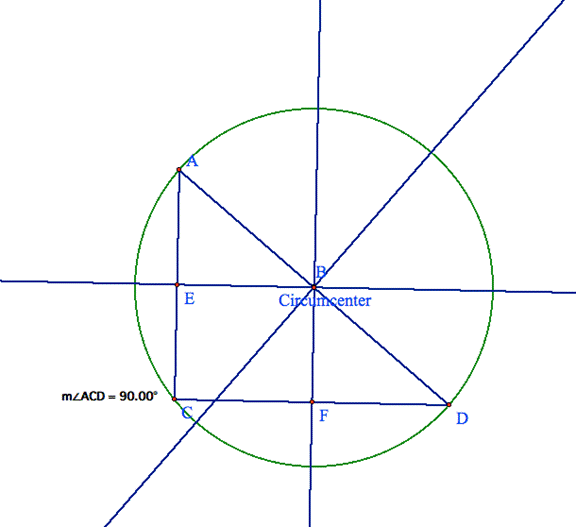
Notice
that the triangle is inside the circle and the circumcenter is in the center of
the circle.† From our first statement we
proclaimed that the circumcenter is equidistant from each vertex therefore we
must conclude that we can create a circle where the segment from the
circumcenter to each vertex is a radii of the circle.
Now
itís your turn click here to open a GSP sketch
to investigate the circumcenter of a circle
The
bigger question is ďWhy is the circumcenter equidistant from each vertex and
though we have shown it, how would we prove it?Ē