 Image
Source: Wikipedia
Image
Source: WikipediaPenrose Tilings
Kyle Schultz
MATH 7200
This webpage provides an introduction to Penrose Tilings and their properties. Discovered by Roger Penrose (1931- ), a British physicist and cosmologist, these tilings are non-periodic and incorporate properties of the Golden Ratio.
Tilings
A tiling is created when a collection of plane figures (tiles) fills a plane such that no gaps occur between the tiles and no two tiles overlap each other. Tilings can be either periodic or non-periodic.
Periodic Tilings
A periodic tiling repeats itself at regular intervals. If you are able to outline a region of the tiling with a parallelogram and then tile the rest of the plane by translating that parallelogram (rotations and reflections are not allowed), then the resulting tiling is periodic. Examples of periodic tilings include regular tessellations, tilings that use only congruent regular polygons (such as regular hexagons,shown below)
 Image
Source: Wikipedia
Image
Source: Wikipedia
and many of patterns featured in the art of M.C. Escher (as shown in the inset of Reptiles below).
 Image
Source: Wikipedia
Image
Source: Wikipedia
Martin Gardner (1989) provides an insightful way to think of periodic tilings: "Think of the plane as being covered with transparent paper on which each tile is outlined. Only if the tiling is periodic can you shift the paper, without rotation, to a new position where all the outlines again exactly fit." (p. 1)
Non-Periodic Tilings
Any tiling that is not periodic is called non-periodic. There are many interesting kinds of non-periodic tilings. Some use congruent shapes, others have self-similar properties, etc. (see Paul Bourke's page on non-periodic tilings for numerous examples).
In most cases, the tiles used in these tilings could also be used to create a periodic tiling. There are, however, some tiles that force a non-periodic configuration. No matter how these tiles are arranged, a periodic tiling cannot be achieved. Penrose Tilings use such tiles.
Penrose Tilings - Kites and Darts
One pair of tiles that Penrose used in his search for tiles that had 5-fold symmetry and tiled the plane were the "dart" and "kite". These tiles are created by partitioning a particular rhombus in the manner depicted in the figure below (the kite appears in yellow, while the dart is purple. Note that the Golden Ratio phi is present in the ratio between the tiles' side lengths.
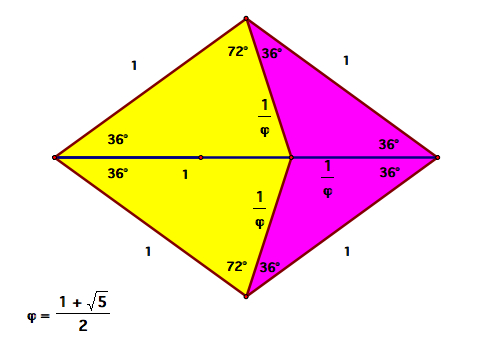
The construction of this pentagon is rather simple, provided that you can construct a regular pentagon. Once a regular pentagon has been constructed, construct its diagonals. These diagonals form a second smaller regular pentagon. Construct the diagonals of this pentagon as well. The rhombus above can be constructed from any two consecutive sides of the original pentagon. Click Here for a Geometer's Sketchpad Sketch detailing this construction.
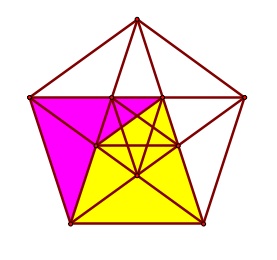
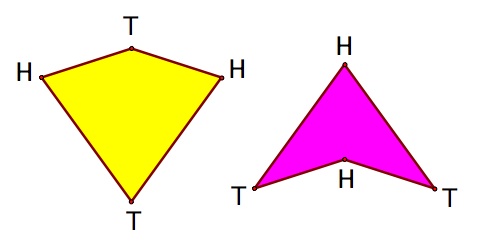
One might observe that, as presented above, the kite and dart could be used to generate a periodic tiling by simply sliding the rhombus in a direction and distance corresponding to its sides. (After all, a rhombus is a parallelogram.) To enable these tiles to force a non-periodic tiling, other measures had to be taken. Penrose and John Horton Conway, a mathematician from Princeton, derived rules for arranging the tiles. The simplest way to state these rules are that, if the vertices of the tiles were to be labeled heads (H) and tails (T) as shown below, then only vertices of the same type could coincide.
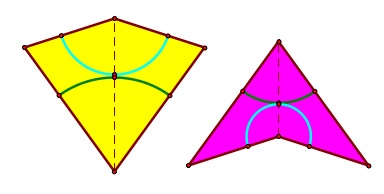
A more visually interesting way of describing the rule for arranging these tiles is to create two distinct paths on the pieces. Each path is portrayed on a tile as an arc of a circle with a distinct color. In order for two tiles to be adjacent, paths of the same colors must be joined.
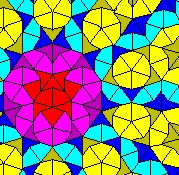
The dart and kite tiles produce some interesting and sometimes beautiful images. The patterns below represent a very small sample.
 Image
source: http://www.uwgb.edu/DutchS/symmetry/penrose.htm
Image
source: http://www.uwgb.edu/DutchS/symmetry/penrose.htm
 Image
source: http://www.flickr.com/photos/tiwonge/1678157943/
Image
source: http://www.flickr.com/photos/tiwonge/1678157943/
 Image
source: http://www.uwgb.edu/DutchS/symmetry/penrose.htm
Image
source: http://www.uwgb.edu/DutchS/symmetry/penrose.htm
Several webpages provide software for creating Penrose Tilings . One of these provides a Java Applet that enables you to work with kites and darts.
Rhombic Penrose Tilings
A second set of Penrose tiles, composed of a "fat" rhombus and a "thin" rhombus, can be constructed from the nested pentagons described above.Note that an additional parallel segment needs to be constructed for the fat rhombus.
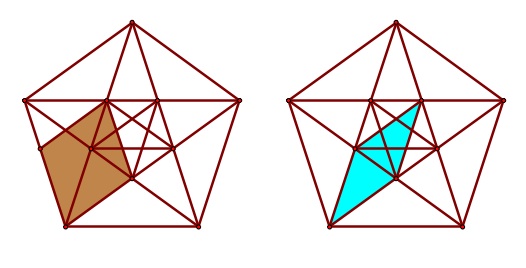
As with the kites and darts above, these tiles must be connected according to a rule that forces non-periodicity. In this case, the red tabs may only touch other red tabs and the green tabs only touch other green tabs.

For some examples of tilings with rhombic tiles, visit Stephen Collins's webpage (which also has a Penrose generator that you can download) or the Penrose webpage at Science U.
Penrose Tilings and the Golden Ratio
As seen above, the ratio of side lengths within the kite and the dart are related to the Golden Ration phi. A Golden relationship can also be found within the rhombic tiles. For the fat rhombus with side length is 1, the length of the long diagonal is phi. For the thin rhombus with side length 1, the length of the short diagonal is 1/phi.
Even more interesting is the relationship between the number of tile types found in one of these tilings. Whereas the tiler has some choice in terms of the arrangement of the tiles, certain configurations necessitate the placement of one type of tile over another. Thus, the number of each type of tiles used is not determined by the tiler, but rather is governed by the geometric properties of the tiles themselves. In fact, the ratio between the number each type of tile used, both in the case of a kite/dart or rhombic tile configuration, approaches phi as the entire plane is tiled. Stated mathematically:
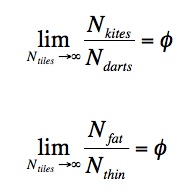
This suggests an interesting activity for students. In small groups, they could create a tiling using either set of tiles, recording how many of each tile is used after different stages (10 total tiles, 50 total tiles, 100 total tiles, etc.). The following links allow you to download pdf templates for Rhombic Tiles and Kites and Darts.
Resources
Books:
Gardner, M. (1989). Penrose tiles to trapdoor ciphers ... and the return of Dr. Matrix. Washington, DC: The Mathematical Association of America.
Livio, M. (2002). The golden ratio: The story of phi, the world's most astonishing number. New York: Broadway Books.
Websites:
Paul Bourke's webpage on non-periodic tilings: http://local.wasp.uwa.edu.au/~pbourke/texture_colour/nonperiodic/
Penrose Darts and Kites Generator Applet: http://www.geocities.com/SiliconValley/Pines/1684/Penrose.html
Rhombic Tilings by Stephen Collins: http://www.stephencollins.net/web/penrose/
The Geometry Junkyard: http://www.ics.uci.edu/~eppstein/junkyard/penrose.html
Rhombic Tilings at Science U: http://www.scienceu.com/geometry/articles/tiling/penrose.html
Return to Kyle Schultz's Homepage