

Alex Szatkowski
This exploration will take a look at pedal triangles and what happens when the pedal point is the centroid, incenter, orthocenter, circumcenter, as well as the center of the 9 point circle of the original triangle.
First let's take a look at what a pedal triangle looks like. A pedal triangle can be easily constructed using GSP. A pedal triangle is created by joining the intersections of lines perpindicular to each of the three sides of the triangle. Lets see what this looks like:
Pedal point outside triangle
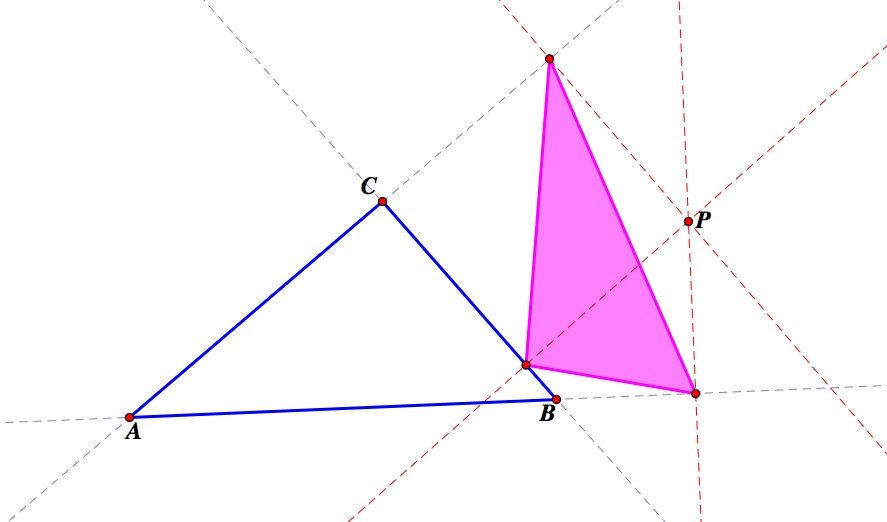
Pedal point inside triangle
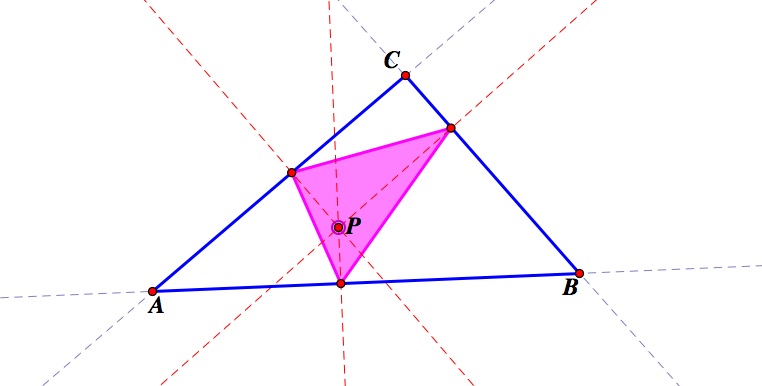
Click here to find a GSP tool for Pedal triangles.
To begin we need to look at the three different types of triangles; acute, obtuse and right to see if there are any differences.
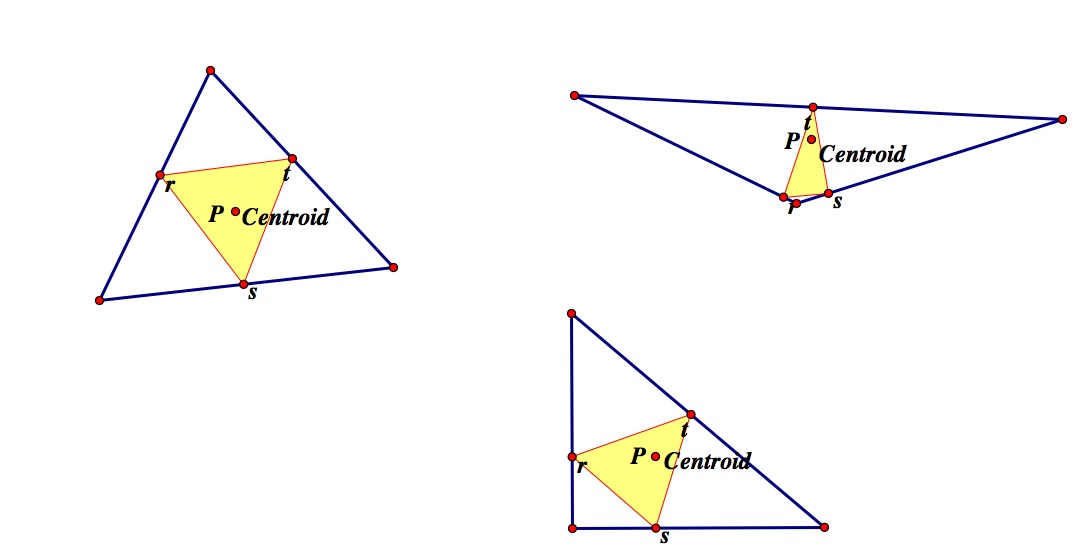
As we can see from the pictures above, when the pedal point is also the centroid of the triangle, the pedal triangle is always completely inside the original triangle.
We will look at the same three types of triangles, acute, obtuse and right.
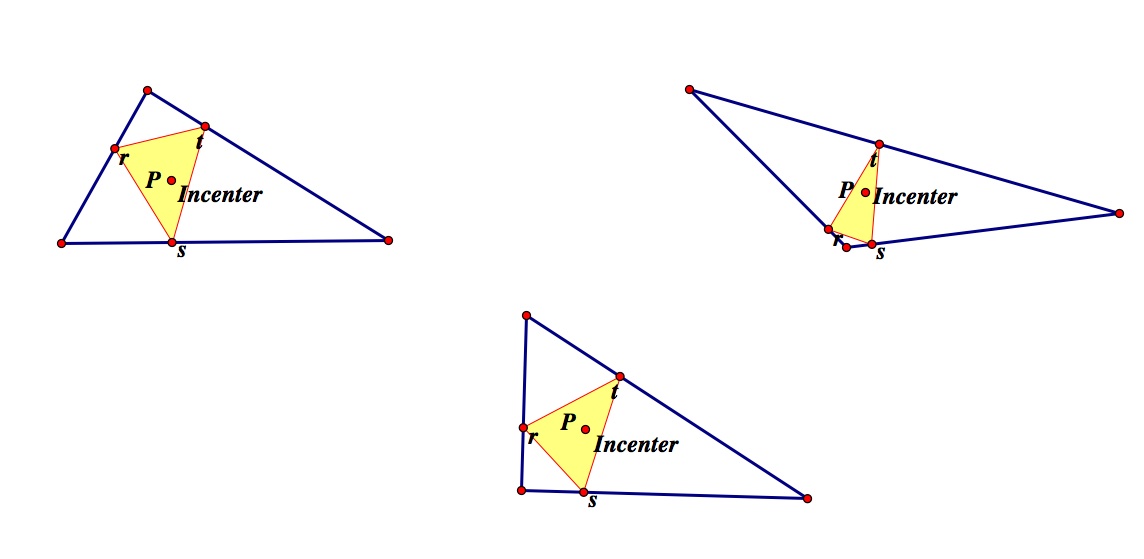
Similar to when the pedal point was also the centroid, when the pedal point is also the incenter, the pedal triangle is always completely inside the original triangle.
Unlike the centroid and incenter, the orthocenter of a triangle is not always inside the triangle so we need to make sure we look at that case.
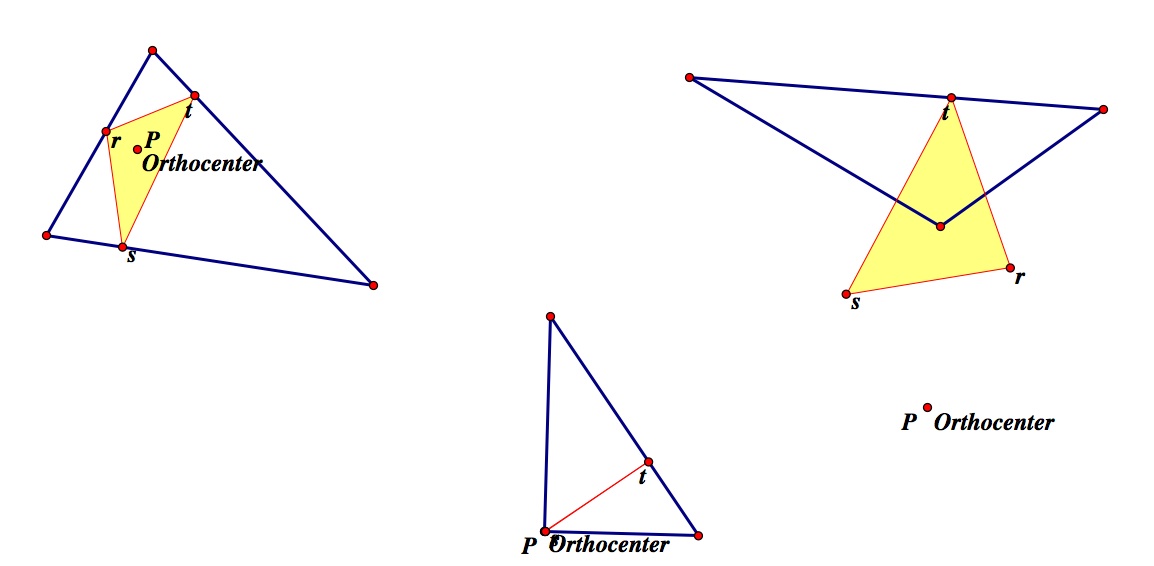
We can make three unique observations:
a. When the triangle is acute, the orthocenter is inside as well as the entire pedal triangle.
b. When the triangle is obtuse, the orthocenter is outside and the pedal triangle overlaps the triangle.
c. When the triangle is right, the orthocenter is at the right angle and the pedal triangle appears as a line. This line is called the Simson Line and is where the three vertices of the pedal triangle are collinear. This is a potential extension to this exploration.
Similar to the orthocenter the circumcenter can be both inside and outside the triangle. Lets see if we get similar results.
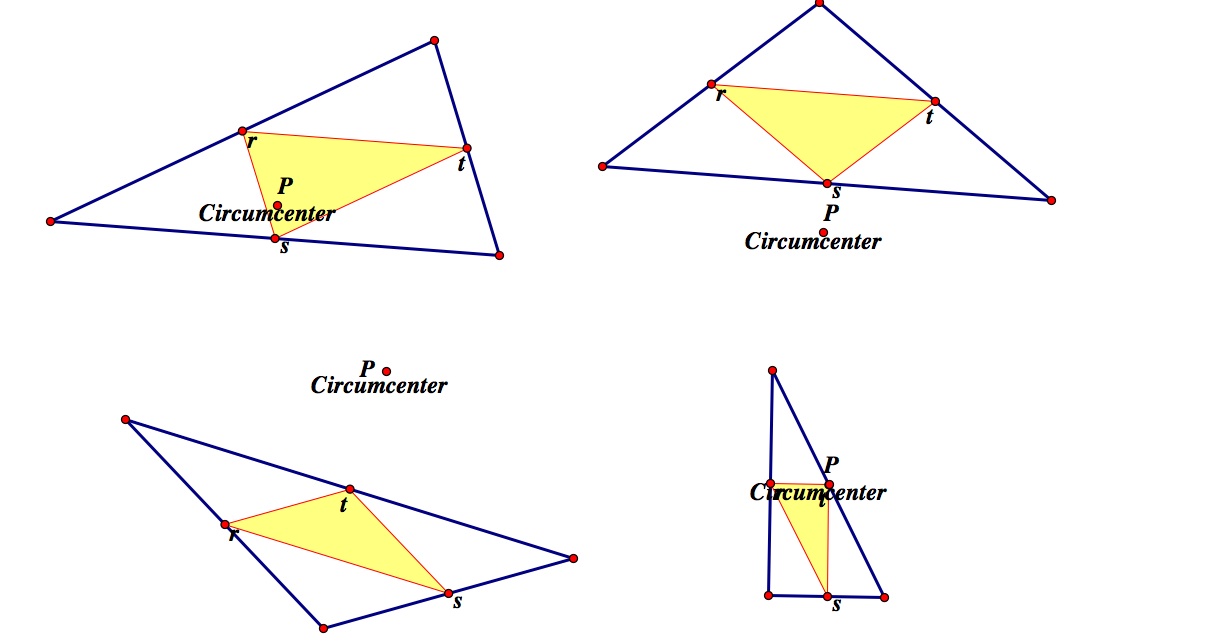
Some observations:
a. Unlike with the orthocenter, when the pedal point was also the circumcenter the pedal triangle was always inside the original triangle.
b. When the triangle was acute, the circumcenter could be inside or outside the triangle as we can see in the top two triangles, however both times the pedal triangle remains inside.
c. In the last picture, the right triangle, the circumcenter, also fell on one of the vertices of our pedal triangle.
We will take a look at an acute, obtuse and right triangle.
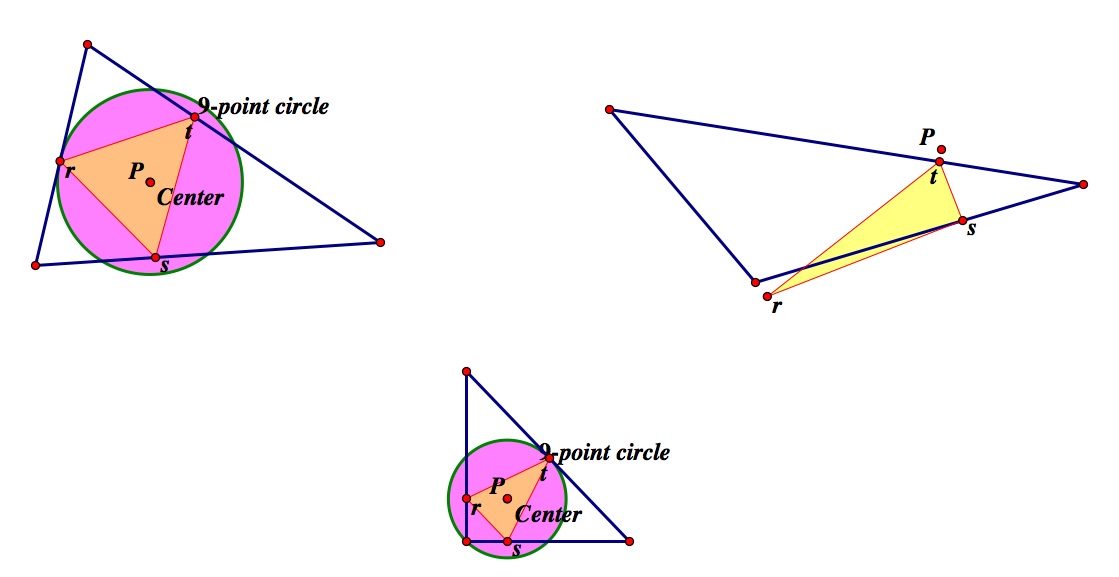
Some observations:
a. For both the acute and right triangles the pedal triangle is completely inside the original triangle.
b. The obtuse triangle does not have a 9-point circle, therefore we cannot investigate what the pedal triangle would look like when the pedal point is the same as the center of the 9 point circle.
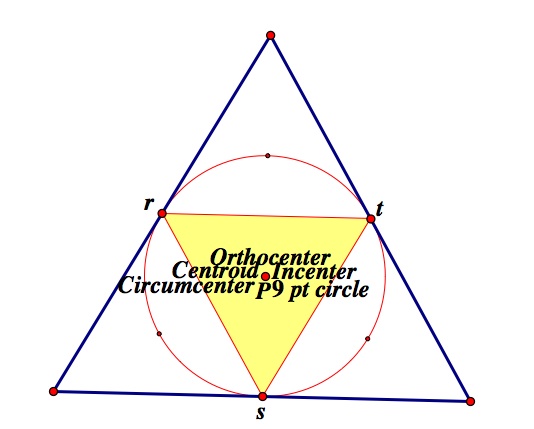
The pedal triangle is always inside the original triangle.