

Last modified on July 25, 2013
These explorations are a set of activities to help become familiar with GSP and to review some basic triangle geometry. After examining the explorations, pick some topic for a brief write-up. The write-up could be one of the proofs, but does not have to be. It could be some exploration you would try with students. Or you might take one of the topics (e.g. medians) and explore some of the standard geometry for the topic. Again the write-up is about the mathematical ideas, not just the pictures.
1. The CENTROID (G) of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.
Use Geometer's Sketchpad (GSP) to Construct the centroid and explore its location for various shapes of triangles.
Some ideas for write-ups about Centroids:
-- Prove the three medians of a triangle are concurrent and the centroid is
the distance from a vertex to the midpoint of the opposite side.
-- The centroid is sometimes portrayed as the "center of mass" or "center of gravity" of the triangle. What does this mean? How can this idea be developed?
-- The medians divide the triangle into six small triangles. Show that these triangles all have the same area.
-- Show that the concurrency of the medians is a special case of Ceva's Theorem.
-- Prove Ceva's Theorem.
-- Extend the concept of centroid to quadrilaterals. In the quadrilateral there are two different centers of mass.
-- Use the centroid of a triangle to develop and prove a procedure for trisecting a line segment.
2. The ORTHOCENTER (H) of a triangle is the point of concurrency or the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side. (Note: the foot of the perpendicular may be on the extension of the side of the triangle.) It should be clear that H does not have to be on the segments that are the altitudes. Rather, H lies on the lines extended along the altitudes. In some geometry texts the perpendicular LINE is the altitude rather than the segment from the vertex to the foot of the altitude.
Use GSP to construct an orthocenter H and explore its location for various shapes of triangles. (Make sure your construction holds for obtuse triangles.)
Some ideas for write-ups about the Orthocenter
-- Demonstrate and prove that the perpendiculars from a vertex to the line of the opposite side are concurrent.
-- The Orthocenter is the point of concurrency of these three lines perpendicular to the lines along the opposite sides. It is NOT NECESSARILY a point of concurrency of the altitudes. It the above figure on the right, the orthocenter H is outside the triangle (blue) and the three altitude segments are shown -- none of them contain H.
-- Show how the proof of the concurrency of these perpendiculars follows from the proof of a circumcenter as the point of concurrency of the perpendicular bisectors of the side of a triangle.
-- Discuss the locus of the orthocenter as one side of a triangle is fixed and the opposite vertex is moved along a parallel line. Or, along a line that is not parallel. Or, along some other curve?
3. The CIRCUMCENTER (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle. Note: C may be outside of the triangle.
Construct the circumcenter C and explore its location for various shapes of triangles. It is the center of the CIRCUMCIRCLE (the circumscribed circle) of the triangle.
Some ideas for write-ups about the Circumcenter
-- Prove that the perpendicular bisectors to the sides of the triangle are concurrent.
-- Prove that the feet of the perpendiculars from a point on the circumcircle to the sides (perhaps extended) are collinear.
4. The INCENTER (I) of a triangle is the point on the interior of the triangle that is equidistant from the three sides. Since a point interior to an angle that is equidistant from the two sides of the angle lies on the angle bisector, then I must be on the angle bisector of each angle of the triangle.
Use GSP to find a construction of the incenter I and explore its location for various shapes of triangles. The incenter is the center of the INCIRCLE (the inscribed circle) of the triangle.
The EXCENTER is the center of a circle that is tangent to the three lines exended along the sides of the triangle. There are three excircles and three excenters. Use GSP do construct a triangle, its incircle, and its three excircles.
Examine the triangle made by the three excenters of a triangle.
Some ideas for write-ups about incenters and excenters.
-- Prove that the internal angle bisectors of a triangle are concurrent.
-- Prove that an internal angle bisector and the two opposite exterior angle bisectors of a triangle are concurrent.
5. Use GSP to construct G, H, C, and I for the same triangle. What relationships can you find among G, H, C, and I or subsets of them? Explore for many shapes of triangles.
Prove that for any triangle, the orthocenter, centroid, and circumcircle are colinear and the centroid is 2/3 the distance from the orthocenter to the circumcenter.
6. Take any triangle. Construct a triangle connecting the three midpoints of the sides. This is called the MEDIAL triangle. It is similar to the original triangle and one-fourth of its area. Construct G, H, C, and I for this new triangle. Compare to G, H, C, and I in the original triangle.
7. Take any acute triangle. Construct a triangle connecting the feet of the altitudes. This is called the ORTHIC triangle. Construct G, H, C, and I for the orthic triangle. Compare to G, H, C, and I in the original triangle. Can you extend this to right triangles or obtuse triangles?
8. Take an acute triangle ABC. Construct H and the segments HA, HB, and HC. Construct the midpoints of HA, HB, and HC. Connect the midpoints to form a triangle. Prove that this triangle is similar to triangle ABC and congruent to the medial triangle. Construct G, H, C, and I for this triangle. Compare.
9. In the same original triangle, construct the three secondary triangles of Exercises 6, 7, and 8. Construct the circumcircle for each of the secondary triangles. What do you observe? Can you prove your conjecture?
10. The Nine-Point circle for any triangle passes through the three mid-points of the sides, the three feet of the altitudes, and the three mid-points of the segments from the respective vertices to orthocenter. Construct the nine points, locate the center (N) and construct the nine point circle.
11. How is N related to G, H, C, or I for different shaped triangles? Could N be considered as a "center" of the triangle?
12. Construction and Proof of the existence of a nine point circle for any triangle.
The CONSTRUCTION can be simplified further by recognizing that the nine point circle is the IMAGE of the circumcircle of the original triangle and the center of the nine point circle is the IMAGE of the circumcenter of the original triangle.
13. Other "centers" of the triangles. There are MANY other points that could be a special construction as a "center" of the triangle. Although many curriculum writers say or imply that there are only 4 -- e.g. H, C, I, and G -- there are many others. Here are some:
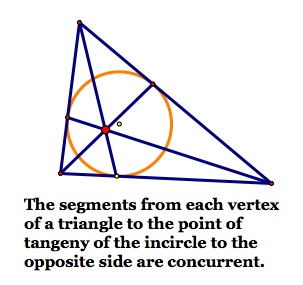
In the first case one should prove that the three line segments are concurrent. Prove.
In the second, a construction is needed to locate such a point. The sum of the distances is minimized but the three angles around the point all have a measure of 120 degrees. Prove. The point is the concurrency of line segments from each vertex to a point outside the opposite side that would be the outer vertex of an equilateral triangle constructed on the side. Prove.