
Bisecting a Triangle
By: Tim Lehman

Exploration 1: Dividing a triangle into
two triangles of equal area
Method I: The most obvious way to divide a triangle into two equal halves is to construct the median from one of the vertices of the triangle to the midpoint of the opposite side, as below. Each of the medians would split the triangle into two equal halves.

Click here if you are wondering why the medians bisect the triangle.
Method II: Other segments exist that divide the triangle into two equal parts. In this section, we will find a segment with not only this charactistic but is also parallel to a side of the triangle.
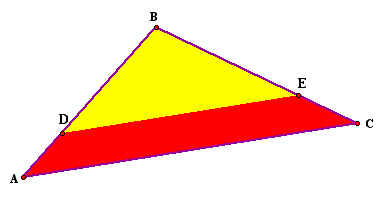
The segment is DE in the above diagram. Need a hint in finding segment DE? For an explanation on how to find DE, click here.
Method III: In this section, we will divide the triangle into pieces are half the triangle when added together. In the drawing below, the triangle has been bisected into the blue quadrilateral and the two green triangles.
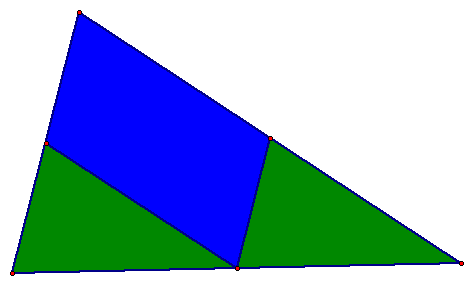
There are several variations of the above diagram. The triangle could be divided in half by selecting two of the four triangles (see diagram below) created by connecting the midpoints of the sides.
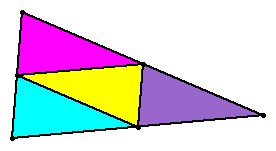
Unsure why this works? Click
here.