

Most people think the Geometer's SketchPad can only be used to help teach geometry. In actuality, the scope of the usability of GSP goes way beyond just that one subject! For example, we can construct the conic sections, topics taught in any algebra class, on Geometer's Sketchpad. Obviously, the first conic section, the circle, is easy to construct from GSP's toolbar and construction menu. But the constructions of the other three conic sections are not so obvious. In this write-up, I show one method of how to construct a parabola, an ellipse, and a hyperbola on the Geometer's Sketchpad. I also allow the reader to use some GSP files to view and explore the trace of the tangent point of each conic section, the trace of the tangent line of each conic section, and the locus of the tangent point of each conic section.
By definition, a parabola is the set of points equidistant from a given point (called the focus) and a given line (called the directrix).
Therefore, to build our parabola on GSP, we need to start with a focus and a directrix. For our purposes, we'll let the directrix be a segment of a line.

Now we can build our parabola.
First, construct a "point on object" on the directrix. Then construct a perpendicular line to the directrix through this point.
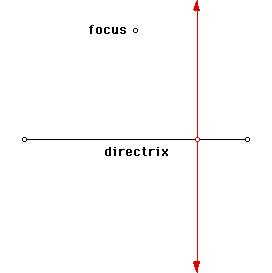
Next, construct a segment from the focus to the point on the directrix. Then construct the midpoint of this segment.
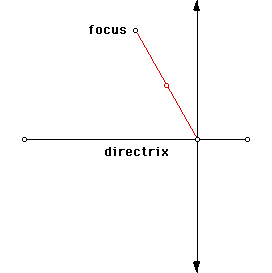
Now construct a perpendicular line to the segment you constructed through its midpoint. Finally, construct the point at the intersection of the first perpendicular line and the perpendicular line you just constructed. This point defines the parabola.
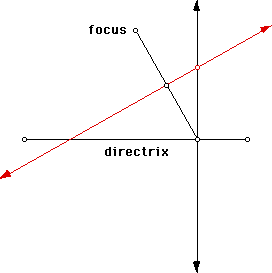
To draw the parabola, trace the point you just created. Then move the point on the directrix along the directrix.
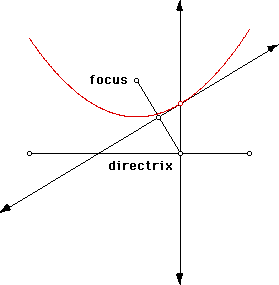
You can let GSP construct the parabola for you if you create an animation button. After setting GSP to trace the tangent point, animate the point on the directrix along the directrix. Click here for a GSP file to view and explore the trace of the tangent point of a parabola.
Another way to construct the parabola is by tracing the tangent line of the parabola. Deselect the trace of the point and instead trace the tangent line of the parabola. Again, you need to move the point on the directrix along the directrix; do this manually, or create an animation button to do the same. Click here for a GSP file to view and explore the trace of the tangent line of a parabola.
**Note that the trace function is only temporary. If you would like your parabola to remain as you investigate (for example) moving the position of the focus and the length of the directrix, you must create a locus of the tangent point. To do this, select the tangent point, and then shift-select the point on the directrix. Go to the GSP Construct Menu and choose "locus." Click here for a GSP file to view and explore the locus of the tangent point of a parabola.
By definition, an ellipse is the set of all points whose sum of their distances from two given points (called the foci) is constant.
Therefore, to build our ellipse on GSP, we need to start with a pair of foci. For our purposes, we'll need to construct a circle and a point inside the circle. The center of the circle and the point inside the circle will be our two foci.
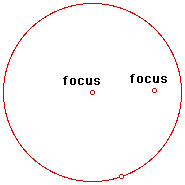
Now we can build our ellipse.
First, construct a "point on object" on the circle (this cannot be the point already on the circle when you drew the circle!). Then construct a line through this point and the center of the circle.
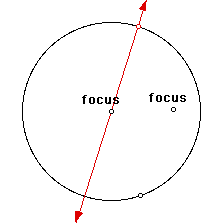
Next, construct a segment from that same point on the circle to the point inside the circle. Then construct the midpoint of this segment.
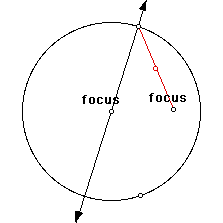
Now construct a perpendicular line to the segment you just constructed through its midpoint. Finally, construct the point at the intersection of the first line you constructed and the perpendicular line you just constructed. This point defines the ellipse.
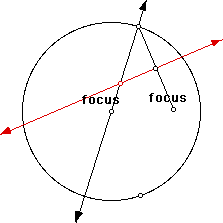
To draw the ellipse, trace the point you just created. Then move the point on the circle along the circle.
You can let GSP construct the ellipse for you if you create an animation button. After setting GSP to trace the tangent point, animate the point on the circle along the circle. Click here for a GSP file to view and explore the trace of the tangent point of an ellipse.
Another way to construct the ellipse is by tracing the tangent line of the ellipse. Deselect the trace of the point and instead trace the tangent line of the ellipse. Again, you need to move the point on the circle along the circle; do this manually, or create an animation button to do the same. Click here for a GSP file to view and explore the trace of the tangent line of an ellipse.
**Note that the trace function is only temporary. If you would like your ellipse to remain as you investigate (for example) moving the positions of the foci and the size of the circle, you must create a locus of the tangent point. To do this, select the tangent point, and then shift-select the point on the circle. Go to the GSP Construct Menu and choose "locus." Click here for a GSP file to view and explore the locus of the tangent point of an ellipse.
By definition, a hyperbola is the set of all points whose difference of their distances from two given points (called the foci) is constant.
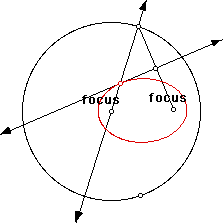
Therefore, to build our hyperbola on GSP, we need to start with a pair of foci. For our purposes, we'll need to construct a circle and a point outside the circle. The center of the circle and the point outside the circle will be our two foci.
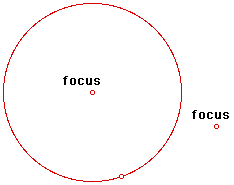
Now we can build our hyperbola.
First, construct a "point on object" on the circle (this cannot be the point already on the circle when you drew the circle!). Then construct a line through this point and the center of the circle.
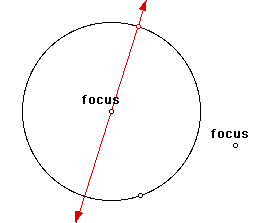
Next, construct a segment from that same point on the circle to the point outside the circle. Then construct the midpoint of this segment.
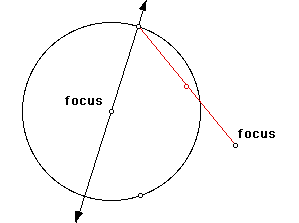
Now construct a perpendicular line to the segment you constructed through its midpoint. Finally, construct the point at the intersection of the first line you constructed and the perpendicular line you just constructed. This point defines the hyperbola.
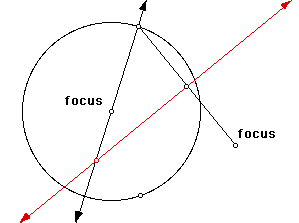
To draw the hyperbola, trace the point you just created. Then move the point on the circle along the circle.
You can let GSP construct the hyperbola for you if you create an animation button. After setting GSP to trace the tangent point, animate the point on the circle along the circle. Click here for a GSP file to view and explore the trace of the tangent point of a hyperbola.
Another way to construct the hyperbola is by tracing the tangent line of the hyperbola. Deselect the trace of the point and instead trace the tangent line of the hyperbola. Again, you need to move the point on the circle along the circle; do this manually, or create an animation button to do the same. Click here for a GSP file to view and explore the trace of the tangent line of a hyperbola.
**Note that the trace function is only temporary. If you would like your hyperbola to remain as you investigate (for example) moving the positions of the foci and the size of the circle, you must create a locus of the tangent point. To do this, select the tangent point, and then shift-select the point on the circle. Go to the GSP Construct Menu and choose "locus." Click here for a GSP file to view and explore the locus of the tangent point of a hyperbola.