

The Liber assumptorum, or Book of Lemmas, is a collection of theorems that reached us through the Arabians. There is reason to believe that many, if not all, of these theorems are actually some of the lost geometrical works of the great mathematician Archimedes. Among these theorems are some properties of the arbelos, or "shoemaker's knife," and the salinon, or the "salt cellar." Four of the properties of the arbelos and one of the salinon will be proved in this essay.
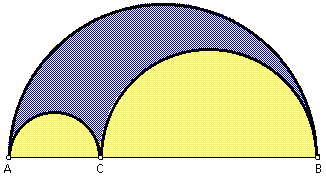
To construct the arbelos:
Let A, C, and B be three points on a straight line, with C lying between A and B. Semicircles are drawn on the same side of the line and having AC, CB, and AB as diameters. The arbelos is the figure bounded by these three semicircles. See figure below (the arbelos is in blue).
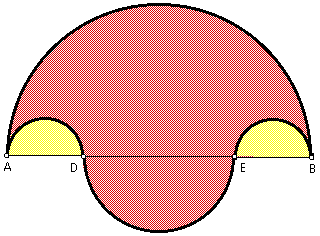
To construct the salinon:
Let A, D, E, and B be four points on a straight line, with D lying between A and E, with E lying between D and B, and with AD = EB. Semicircles are drawn on the same side of the line and having AD, EB, and AB as diameters. A semicircle is drawn on the opposite side of the line and having DE as the diameter. The salinon is the figure bounded by these four semicircles. See figure below (the salinon is in red).
Resource:
Eves, Howard (1992). An Introduction to the History of Mathematics. Saunders College Publishing: Philadelphia, Pennsylvania.
Given the arbelos as described above. At C, construct a perpendicular to AB to cut the largest semicircle in G. Construct GA to cut the semicircle with diameter AC in point X. Construct GB to cut the semicircle with diameter CB in point Y. Prove that quadrilateral GXCY is a rectangle.
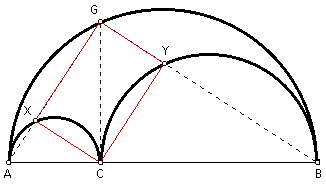
Since triangle AGB is inscribed in a semicircle, and its hypotenuse is the diameter of the semicircle, then triangle AGB is a right triangle. Therefore, angle AGB = 90 degrees. By angle addition and substitution, if angle AGC = a and angle CGB = b, then a + b = 90 degrees.
Since triangle GCB is a right triangle by definition, and since the sum of the angles of a triangle = 180 degrees, then angle GBC = a. Similarly, angle GAC = b.
Since triangles AXC and CYB are inscribed in semicircles, and their hypotenuses are the diameters of the semicircles, then triangles AXC and CYB are also right triangles. Therefore, angles AXC and CYB = 90 degrees. Since the sum of the angles of a triangle = 180 degrees, it follows that angle XCA = a and angle YCB = b.
By angle addition, angle GCY = a and angle GCT = b.
Since GC = GC by reflexivity, it follows that triangles GXC and CYG are congruent by ASA.
By the fact that corresponding sides of congruent triangles are congruent, it follows that XC = YG and GX = CY.
Now, we have that quadrilateral GXCY has both pairs of opposite sides congruent. Thus, quadrilateral GXCY is a parallelogram.
Since by angle addition and substitution, angle XCY = a + b = 90 degrees, and quadrilateral GXCY is a parallelogram, it follows that quadrilateral GXCY is actually a rectangle.
QED.
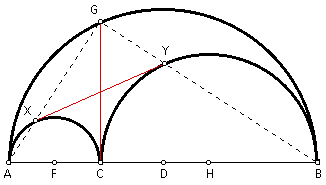
Given the arbelos as described above. At C, construct a perpendicular to AB to cut the largest semicircle in G. Construct GA to cut the semicircle with diameter AC in point X. Construct GB to cut the semicircle with diameter CB in point Y. Construct segment XY. Prove that GC and XY are equal and bisect each other.
By Proof 1 above, quadrilateral GXCY is a rectangle.
Segments GC and XY are diagonals by definition. Since the diagonals of a rectangle are equal and bisect each other, it follows by transitivity that segments GC and XY are equal and bisect each other.
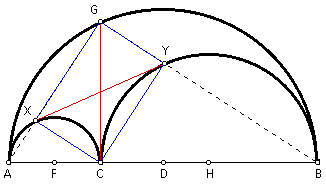
Given the arbelos as described above. At C, construct a perpendicular to AB to cut the largest semicircle in G. Construct GA to cut the semicircle with diameter AC in point X. Construct GB to cut the semicircle with diameter CB in point Y. Construct segment XY. Prove that segment XY is the common tangent to both of the smaller semicircles.
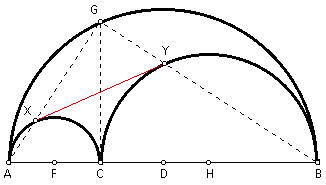
By Proof 1 above, quadrilateral QXCY is a rectangle. Therefore, angle XCY = 90 degrees. By angle addition and substitution, if angle GCY = a and angle GXC = b, then a + b = 90 degrees.
Since angle GCB is a right angle by definition, then by angle addition and substitution, angle YCB = b. Similarly, angle XCA = a.
By Proof 2 above, segments XY and GC are equal and bisect each other. Let the intersection of segments XY and GC be point N. This means that NY = NC = NX. By definition, triangles NCY and NXC are isosceles triangles. Therefore, angle NCY = angle NYC = a and angle NCX = angle NXC = b.
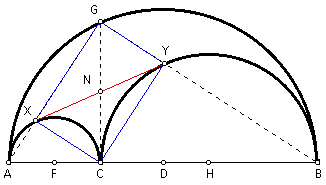
Let point F be the midpoint of segment AC and point H be the midpoint of segment CB. Construct segments FX and HY.
By definition, segments FX and FC are radii of the same semicircle. Also, segments HY and HC are radii of the same semicircle. It follows then that FX = FC and HY = HC.
By definition, triangles FXC and HYC are isosceles triangles. Thus, angle XCF = angle CXF = a and angle YCH = angle CYH = b.
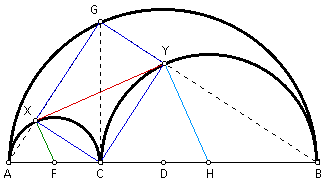
By angle addition and substitution, angle YXF = a + b = 90 degrees and angle XYH = a + b = 90 degrees.
Since FX is a radii of the semicircle with diameter AC, and FX is perpendicular to segment XY, then segment XY is tangent to the semicircle. Similarly, segment XY is tangent to the semicircle with diameter CB.
Thus, segment XY is the common tangent to both of the smaller semicircles.
QED.
Given the arbelos as described above. At C, construct a perpendicular to AB to cut the largest semicircle in G. Prove that the area of the arbelos equals the area of the circle on GC as diameter.
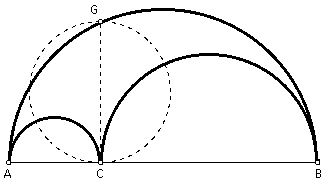
Construct the midpoing of diameter AB and call it D. Construct the midpoint of diameter AC and call it F. Construct the midpoint of diameter CB and call it H. By construction, FA and FC are radii of the same circle, and so FA = FC = x. By construction, HC and HB are radii of the same circle, and so HC = HB = y. By construction, DA and DB are radii of the same circle, and so DA = DB = x + y (Since AB = 2x + 2y). Therefore, CD = y - x and DH = x.
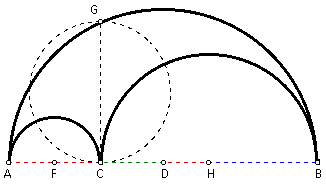
Construct segment DG. By definition, DG is the radii of the semicircle on diameter AB, and so DG = DA = DB = x + y. Since triangle GCD is a right triangle (by definition), then using the Pythagorean Theorem, GC^2 + DC^2 = DG^2. By substitution, GC^2 + (y - x)^2 = (x + y)^2. Using algebra, GC^2 + y^2 - 2xy + x^2 = x^2 + 2xy + y^2, and so GC^2 = 4xy. Solving for GC gives GC = 2*sqrt(xy). Since GC is the diameter of the circle in question, the radius of this circle = (1/ 2)GC = sqrt(xy). Therefore, the area of the circle with diameter GC = pxy.

Finding the area of the arbelos simply requires more algebra. The area of the semicircle with diameter AC = (1/ 2)px^2. The area of the semicircle with diameter CB = (1/ 2)py^2. The area of the largest semicircle (the one with diameter AB) = (1/ 2)p(x + y)^2. Therefore, the area of the arbelos = (1/ 2)p[(x + y)^2 - x^2 - y^2] = (1/ 2)p(x^2 + 2xy + y^2 - x^2 - y^2) = (1/ 2)p(2xy) = pxy.
QED.
Given the salinon as described above. Construct the midpoint of DE and call it O. Construct a perpendicular to DE at O to cut the largest semicircle in C and the semicircle on diameter DE in F. Prove that the total area of the salinon is equal to the area of the circle having for diameter the line FOC of symmetry of the figure.
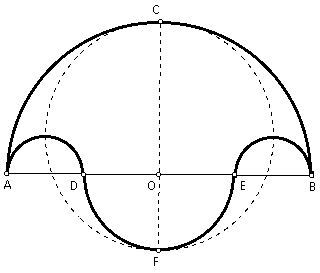
Construct the midpoint of AD and call it G. Construct the midpoint of EB and call it H. Since AD = EB, it follows that AG = GD = EH = HB = x. Since OD, OE, and OF are all radii of the same semicircle, it follows that OD = OE = OF = y. By segment addition, AO = OB = 2x + y, and so O is also the midpoint of diameter AB. Therefore, CF is the line of symmetry of the salinon. Also, since OA, OB, and OC are all radii of the same circle, then OA = OB = OC = 2x + y.

Construct the midpoint of segment CF and call it P. Since OC = 2x + y and OF = y, it follows that CF = 2x + 2y by segment addition. Therefore, the radii of the circle in question is x + y. So the area of the circle = p(x + y)^2
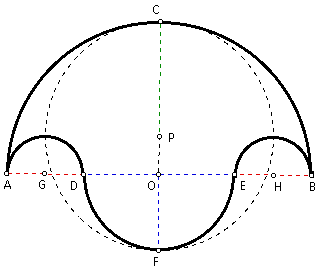
Finding the area of the salinon simply requires more algebra. The area of the semicircle with diameter AB = (1/ 2)p(2x + y)^2. The area of the semicircle with diameter DE = (1/ 2)py^2. The area of each of the semicircles with diameters AD and EB = (1/ 2)px^2. Therefore, the area of the salinon is (1/ 2)p[(2x + y)^2 - 2x^2 + y^2] = (1/ 2)p(4x^2 + 4xy + y^2 - 2x^2 + y^2) = (1/ 2)p(2x^2 + 4xy + 2y^2) = p(x^2 + 2xy + y^2) = p(x + y)^2.
QED.