Super Ellipse
and His Sidekick Astroid

by

D. Hembree

The study of conic sections is common in high school Algebra II and Analysis and, indeed, is a Georgia Quality Core Curriculum requirement for those courses. This page offers resources for an extension or enrichment of the topic of ellipses.

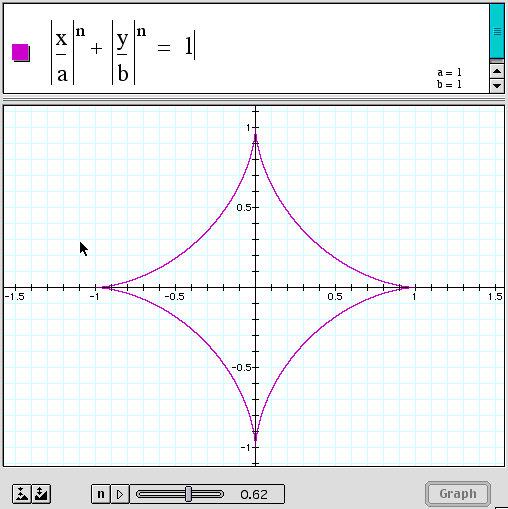
The general form of equations discussed here are known as Lame' curves after the  mathematician Gabriel Lame' (1795-1870), though their study was most advanced by Julius Plucker (1801-1866). As is often the case, Lame's name became associated with these curves because he introduced the notation for their representation. In their modern form, Lame' curves are described by the equation

where n is any positive real number. The standard form for an ellipse is immediately recognizable when n = 2.
Find more about Gabriel Lame' here

When n = 2 and a = b, it should be obvious that the curve represents a circle with radius a (=b), so for our purposes, we consider the circle as just a special case of the ellipse.


As part of  the usual study of ellipses, the roles of a and b are discussed as the x- and y-intercepts of the ellipse. We will not concern ourselves with those roles here. What is seldom considered in a high school course is the role of the exponent n.

What if n takes on some value other than 2? An easy and appropriate tool for investigating this question is Graphing Calculator for the Macintosh (also available with reduced capabilities for the IBM-compatable as NuCalc from Pacific Tech ) or the freeware program for the IBM, Winplot  from Rick Parris at Philips Exeter Academy.

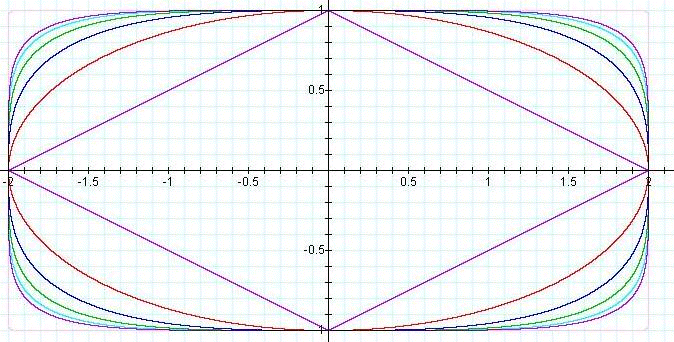
If you are using a Macintosh computer, it already has Graphing Calculator as part of its software. Click anywhere on the image below to open Graphing Calculator and explore how changing the exponent changes the graph of     as n ranges from 1 to 20.
 
 

 As you see, the members of this family of curves are all "ellipse-like", but only the red curve is a true ellipse. For n > 2, the curves are known as super ellipses and have as their limiting case the rectangle formed by the lines |x| = 2 and |y| = 1. The faint lavender curve in the figure above is the graph of  .

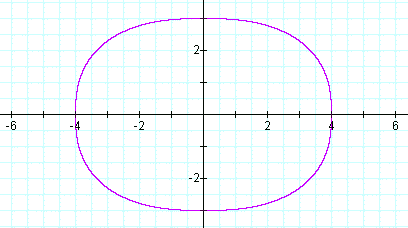
The term super ellipse was coined by the Danish artist, author, designer, and mathematician Piet Hein in the 1970's. He used a super ellipse with n = 2.5 as the design for  tabletops and windows. His preferred choices for a and b in the Lame' equation were in the ratio 4:3. The graph is shown here:

 

Piet Hein is as well known in Scandinavia as is Hans Christian Andersen and has streets, parks and buildings named for him in several major cities. When asked to design a plaza for the city of Stockholm, he used his super ellipse as its basis, enhancing traffic flow as well as creating an estheticly pleasing fountain.

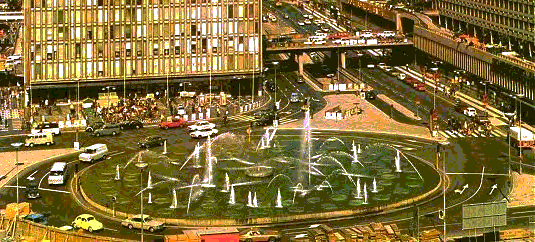
Hein also marketed a three dimensional version of his super ellipse, which he called a super egg.  The super egg is formed by rotating a super ellipse about its longer axis and is interesting because of  its remarkable stability when balanced on its end. In the 1970's wooden models were popular in Europe and today, items such as this Stress Egg are available.



In the Lame' equation, if the exponent is 2/3, the resulting curve is known as an astroid (NOT asteroid) similar to the graph shown below with n = .62. If you would like to explore with other values of n, click on the figure to open Graphing Calculator. An astroid may also be produced by finding the locus of points on a circle as the circle rolls around the inside of another circle with four times its diameter. To see an animation of this in Geometer's Sketchpad, click here.


Return to D. Hembree's EMAT 6680 page
Email to dhembree@coe.uga.edu