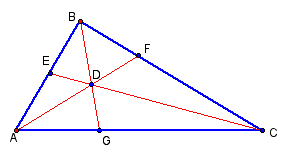
We will begin with a verification of Ceva's Theorem.

 

Given triangle ABC with cevians BG, AF and CE concurrent at point D, we wish to demonstrate that:

Click here for a GSP 4.0 sketch to investigate.

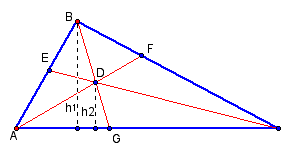
We begin by constructing altitudes h1 and h2. The area of triangle ABG [in the future, we will use the notation (ABG) to designate the area of triangle ABG] equals 0.5(AG)(h1) and (BGC) = 0.5(GC)h1. Also, (ADG) = 0.5(AG)(h2) and (DGC) = 0.5(GC)(h2). Thus,

We conclude, then, that

Similar reasoning yields the equations

.

Thus,

By cancelation,

---

We will now consider the converse of Ceva's theorem.

Given,

,

show that cevians BG, AF and CE are concurrent.

Click here for a GSP 4.0 sketch to manipulate.

Assume that cevians AF and CE intersect at D, and that the other cevian through D is BH. By Ceva's theorem,

.

Since we assumed

,

by the transitive property,

.

Simplifying,

,

which is true only if H and G represent the same point. Thus, segments AF, CE and BG must be concurrent.