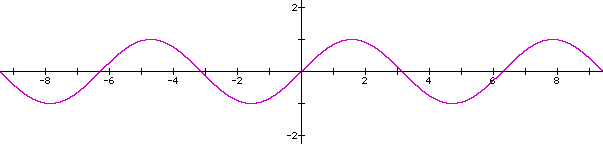
We will examine the function y = asin(bx + c) for different values of a, b and c. We will begin by graphing y = sinx (a, b, c = 1). The remainder of the graphs will be compared to this form of the function:
y = sinx

The next few graphs demonstrate what happens when a is varied. Notice that the amplitude of the curve (distance of the maximum and minimum points from the x-axis) varies according to the change in this coefficient.
y = sin x
y = 3sinx
y = 0.5 sinx
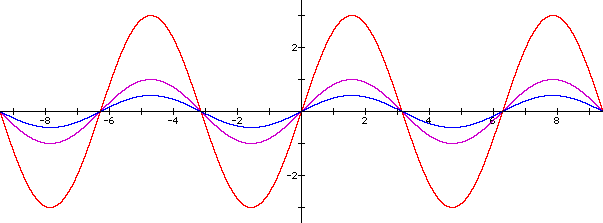
Notice that when a = 3 (graphed in red), the amplitude of the curve is 3. Likewise, when a = 0.5 (graphed in blue), the amplitude is 0.5.
It is worth noting that if a is negative, the graph is reflected across the x-axis. This is demonstrated by the following graphs of y = 2sinx and y = -2sinx.
y = sinx
y = 2sinx
y = -2sinx
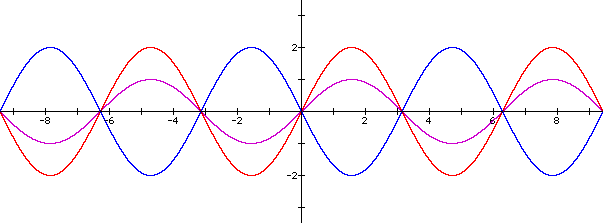
Notice that the graph of y = -2sinx (graphed in blue) has an amplitude of 2 and is the reflection of y = 2sinx (graphed in red).
We will now demonstrate the effect of varying b while a and c remain constant. The following graphs indicate the result of letting b = 1, 2 and 0.5 while a = 1 and c = 0:
y = sinx
y = sin2x
y = sin0.5x
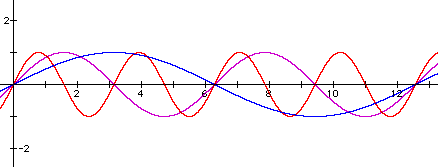
It is evident that changing b affects the period of the sine function. Specifically, the period of each function is equal to the absolute value of 2p/b. Notice that when b = 1 (graphed in pink), the period is equal to 2p/1 = 2p, or about 6.3. When b = 2 (graphed in red), the period equals 2p/2 = p which is about 3.1. When b = 0.5 (graphed in blue), the period equals 2p/0.5 = 4p or about 12.6.
We will conclude by investigating the effect of changing c while holding a and b constant. In the following graphs, a and b will remain equal to 1 while c = 0, 1 and -2.
y = sinx
y = sin(x + 1)
y = sin(x - 2)
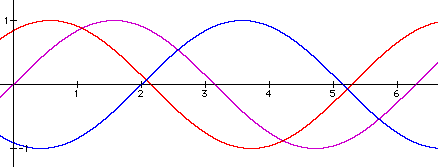
Changing c effectively shifts the graph to the left or to the right. This phase shift is determined by -c/b. For example, when c = 1 (graphed in red), the graph has the same period and amplitude as when c = 0 (graphed in pink), but has been shifted -(1/1) = -1, or 1 unit to the left. When c = -2 (graphed in blue), the graph also has the same amplitude and period as the graph of y = sinx, but it has been shifted -(-2/1) = 2 or 2 units to the right.